Maatriks

m × n maatriks: m rida on horisontaalsed ja n veergu on vertikaalsed. Maatriksi iga elementi tähistatakse sageli kahe alaindeksiga tähega. Näiteks a_2,1 tähistab teises reas ja esimeses veerus paiknevat elementi

Maatriks on matemaatiline objekt, mida esitatakse ristkülikukujuline (ridadeks ja veergudeks jaotatava) tabelina, mis koosneb numbritest, sümbolitest või avaldistest, mis tähistavad arve (tavaliselt reaalarve või kompleksarve) või mingeid muid etteantud hulka kuuluvaid matemaatilisi objekte, näiteks polünoome, funktsioone, diferentsiaale, vektoreid. Objekte, mida tabeli sissekanded tähistavad, nimetatakse maatriksi elementideks või maatriksi komponentideks.

Tavaliselt eeldatakse, et selle hulga elemente, millest maatriksi elemendid võetakse, saab liita ja lahutada sarnaselt arvudega (nad moodustavad Abeli rühma). Lineaaralgebras eeldatakse tavaliselt ka, et neid saab arvude kombel korrutada ja jagada: nad moodustavad korpuse või üldisemalt ühikelemendiga assotsiatiivse ringi. Tehted maatriksitega defineeritakse maatriksi elementide tehete (liitmine ja lahutamine, korrutamine ja jagamine) kaudu.

Et osutada sellele, kust maatriksi elemendid võetakse, räägitakse maatriksist üle mingi hulga, ringi või korpuse (näiteks reaalarvuliste elementidega maatriksit nimetatakse maatriksiks üle reaalarvude korpuse).

Maatriksid kuuluvad lineaaralgebra kesksete objektide hulka. Maatrikseid kasutatakse näiteks lineaarvõrrandisüsteemide lahendamisel.

Maatrikseid uurib maatriksite teooria.

Maatriksi üldistus on hüpermaatriks, millel võib olla rohkem mõõtmeid kui 2.

Definitsioonid ja tähistused

Maatriks on matemaatiline objekt, mida esitatakse ristkülikukujuline (ridadeks ja veergudeks jaotatava) tabelina, mis koosneb numbritest, sümbolitest või avaldistest, mis tähistavad arve või muid matemaatilisi objekte. Näiteks

$A=\left(\begin{array}{ccc}1& 2& 3\\ 1& 2& 7\\ 4& 9& 2\\ 6& 0& 5\end{array}\right)$

on maatriks. Objekte, mida maatriksi kui tabeli sissekanded tähistavad, nimetatakse maatriksi elementideks ehk maatriksi komponentideks.

Maatriksi mõõtmed määratakse selle ridade ja veergude arvuga. Kui maatriksil on m rida ja n veergu, siis nimetatakse seda m × n (m-korda-n) järku maatriksiks või lihtsalt m × n maatriksiks. Positiivsete täisarvude järjestatud paari m × n nimetatakse 'maatriksi järguks ehk mõõtmeteks ehk dimensiooniks ehk suuruseks ning arve m ning n selle mõõtmeteks ehk dimensioonideks. Ülal on kujutatud 4 × 3 maatriksit. (Mõnikord vaadeldakse ka lõpmatuid maatrikseid, millel on lõpmata palju ridasid ja veerge, ja tühje maatrikseid, mille ridade arv või veergude arv või mõlemad on 0.)

Maatriksit, mille ridade arv võrdub veergude arvuga, nimetatakse ruutmaatriksiks. n × n ruutmaatriksi järguks loetakse lihtsalt arvu n.

Maatriksit, mille üks mõõtmetest võrdub ühega, nimetatakse ka vektoriks. Täpsemalt, maatrikseid dimensioonidega 1 × n ja m × 1 nimetatakse vastavalt reavektoriteks ja veeruvektoriteks. Näiteks

$A=\left(\begin{array}{ccc}1& 2& 3\end{array}\right)$

on 1 × 3 reavektor.

Elemendi kohta, mis asub maatriksi i-ndas reas ja j-ndas veerus, öeldakse, et see element asub kohal i-j.

Maatrikseid tähistatakse suurte ladina tähtedega ning elemente tavaliselt väikeste ladina või kreeka tähtedega, mis on varustatud kahe asukohale viitava alaindeksiga (näiteks a₁₁ või a_1,1, kusjuures esimene indeks viitab reale ja teine veerule. m × n maatriksit

$A=\left(\begin{array}{cccc}{a}_{11}& a_{12}& \dots & a_{1n}\\ a_{21}& a_{22}& \dots & a_{2n}\\ \dots & \dots & \dots & \dots \\ a_{m1}& a_{m1}& \dots & a_{mn}\end{array}\right)=\left(\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right)$

esitatakse lühidalt üldelemendi a_ij abil: $$𝐀=\left(a_{ij}\right),\left[a_{ij}\right],\text{või}{\left(a_{ij}\right)}_{1\le i\le m,1\le j\le n}$$ või ka $𝐀=(a_{i,j}{)}_{1\le i,j\le n}$, kui $n=m$. Kasutusel on ka tähistus, mille puhul maatriksi elementi tähistatakse sama sümboliga kui maatriksit ennast, näiteks (A)_ij või ka sulgudeta A_ij. Maatriksite eristamiseks teistest objektidest kasutatakse ka näiteks rasvast kirja (A) või kahekordset allakriipsutamist ($\underset{\_}{\underset{\_}{A}}$).

Maatriksi A elementi i-ndas reas ja j-ndas veerus nimetatakse mõnikord maatriksi i,j-elemendiks või (i, j) elemendiks ning tähistatake tavaliselt a_i,j või a_ij, mõnikord A[i,j] või A_i,j. Näiteks järgneva maatriksi A (1, 3) element (a₁₃, a_1,3, A[1,3], A_1,3) on 5:

$𝐀=\left[\begin{array}{cccc}4& -7& 5& 0\\ -2& 0& 11& 8\\ 19& 1& -3& 12\end{array}\right]$.

Mõnikord antakse maatriksi elemendid valemiga: a_i,j = f(i, j). Näiteks järgneva maatriksi A elemendid on antud valemiga a_ij = i − j.

$𝐀=\left[\begin{array}{cccc}0& -1& -2& -3\\ 1& 0& -1& -2\\ 2& 1& 0& -1\end{array}\right]$

Sel juhul antakse maatriks ise mõnikord selle valemiga nurksulgudes või topeltsulgudes, näiteks siinsel juhtumil A = [i−j] või A = ((i−j)). Kui maatriksi mõõtmed on m × n, siis valem f(i, j) kehtib, kui i = 1, ..., m ja j = 1, ..., n. Seda võib eraldi mainida või anda m × n alakirjas, meie juhtumil A = [i − j] (i = 1, 2, 3; j = 1, ..., 4) või A = [i − j]_3×4.

Maatriksi ridu ja veerge tähistatakse mõnikord tärni abil, näiteks a_i,∗ on maatriksi A i-s rida ja _a∗,j on maatriksi A j-s veerg.

Maatrikseid, mille elemendid kuuluvad ringi R, nimetatakse maatriksiteks üle ringi R. Näiteks maatrikseid, mille elementideks on reaalarvud, nimetatakse maatriksiteks üle reaalarvude korpuse või üle reaalarvude.

Tehted maatriksitega

Liitmine, korrutamine skalaariga ja transponeerimine

Lihtsaimad tehted maatriksitega on maatriksite liitmine, skalaariga korrutamine ja transponeerimine.

Tehe	Definitsioon	Näide
Liitmine	Olgu A ja B m × n maatriksid üle ringi R. Siis A ja ''B summa A+B vahel leitakse elementhaaval: (A + B)ij = Aij + Bij, kus 1 ≤ i ≤ m and 1 ≤ j ≤ n.	$\left(\begin{array}{ccc}1& 3& 1\\ 1& 0& 0\end{array}\right)+\left(\begin{array}{ccc}0& 0& 5\\ 7& 5& 0\end{array}\right)=\left(\begin{array}{ccc}1+0& 3+0& 1+5\\ 1+7& 0+5& 0+0\end{array}\right)=\left(\begin{array}{ccc}1& 3& 6\\ 8& 5& 0\end{array}\right).$
Skalaariga korrutamine	Maatriksi A korrutamisel skalaariga c korrutatakse kõiki maatriksi elemendid ükshaaval läbi skalaariga c: Mall:Murdmata	$2\cdot \left(\begin{array}{ccc}1& 8& -3\\ 4& -2& 5\end{array}\right)=\left(\begin{array}{ccc}2\cdot 1& 2\cdot 8& 2\cdot -3\\ 2\cdot 4& 2\cdot -2& 2\cdot 5\end{array}\right)=\left(\begin{array}{ccc}2& 16& -6\\ 8& -4& 10\end{array}\right).$
Transponeerimine	m × n maatriksi A transponeeritud maatriks AT on n × m maatriks, mis saadakse veergude ja ridade äravahetamisel: Mall:Murdmata	${\left(\begin{array}{ccc}1& 3& 1\\ 0& -6& 0\end{array}\right)}^T=\left(\begin{array}{cc}1& 0\\ 3& -6\\ 1& 0\end{array}\right)$

Skalaariga korrutamise omadused ja liitmise omadused (assotsiatiivsus ja kommutatiivsus) ringis kanduvad üle maatriksite liitmisele: näiteks A + B = B + A.

Transponeerimise tehe, mida arvude (või ringi elementide) jaoks ei eksisteeri, ühildub liitmise ja skalaariga korrutamisega kui (cA)^T = c(A^T) ja (A + B)^T = A^T + B^T. Veel kehtib (A^T)^T = A.

Korrutamine

Üldistatud kuju meeldetuletusega, et esimese maatriksi ridade arv peab võrduma teise maatriksi veergude arvuga

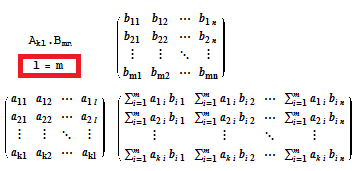
Kahte maatriksit saab korrutada vaid siis, kui esimese teguri veergude arv on võrdne teise teguri ridade arvuga. Kui A on m × n maatriks ja B on n × p siis AB on m × p maatriks, mille elemendid on

$(AB{)}_{ij}=(A{)}_{i1}(B{)}_{1j}+(A{)}_{i2}(B{)}_{2j}+\dots +(A{)}_{in}(B{)}_{nj}=\sum _{k=1}^n(A{)}_{ik}(B{)}_{kj}$

iga i = 1,2 ... m ja j = 1,2 ... p korral.

Näiteks

$\left(\begin{array}{ccc}1& 0& 2\\ -1& 3& 1\end{array}\right).\left(\begin{array}{cc}3& 1\\ 2& 1\\ 1& 0\end{array}\right)=\left(\begin{array}{cc}1\cdot 3+0\cdot 2+2\cdot 1& 1\cdot 1+0\cdot 1+2\cdot 0\\ -1\cdot 3+3\cdot 2+1\cdot 1& -1\cdot 1+3\cdot 1+1\cdot 0\end{array}\right)=\left(\begin{array}{cc}5& 1\\ 4& 2\end{array}\right).$

ja sarnaselt

$\left(\begin{array}{cc}3& 1\\ 2& 1\\ 1& 0\end{array}\right).\left(\begin{array}{ccc}1& 0& 2\\ -1& 3& 1\end{array}\right)=\left(\begin{array}{ccc}2& 3& 7\\ 1& 3& 5\\ 1& 0& 2\end{array}\right)$

Maatriksite korrutamine on:

• assotsiatiivne: (AB)C = A(BC)
• distributiivne: (A + B)C = AC + BC ja C(A + B) = CA + CB

Kui korrutis AB on defineeritud, ei pruugi korrutis BA defineeritud olla. Täpsemalt on mõlemad korrutised defineeritud parajasti siis, kui A ja B on sama järku ruutmaatriksid. Ka siis, kui AB ja BA on defineeritud, ei pruugi need korrutised võrdsed olla, st üldjuhul

AB ≠ BA.

st erinevalt reaal- või kompleksarvude korrutamisest pole maatriksite korrutamine kommutatiivne.

Pöördmaatriks

Ruutmaatriksi A pöördmaatriksiks nimetatakse maatrksit B, mis rahuldab tingimust

$AB=BA=I,$

kus I on ühikmaatriks. Pöördmaatriksit tähistatakse sümboliga $A^{-1}$. Ruutmaatriksil leidub pöördmaatriks parajasti siis, kui selle determinant on nullist erinev ehk kui see on regulaarne. Maatriksi A pööramiseks nimetatakse tehet, mis seisneb ülalantud tingimust rahuldava maatriksi B leidmises.

Rakendused lineaaralgebras

Maatriksid tekivad loomulikul moel lineaarvõrrandisüsteemide lahendamisel ja lineaarteisenduste vaatlemisel.

Lineaarvõrrandisüsteemid

Vaatleme lineaarvõrrandisüsteemi kujul:

$\{\begin{array}{c}{a}_{11}{x}_1+a_{12}{x}_2+\dots +a_{1n}{x}_n=b_1\\ a_{21}{x}_1+a_{22}{x}_2+\dots +a_{2n}{x}_n=b_2\\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\ a_{m1}{x}_1+a_{m2}{x}_2+\dots +a_{mn}{x}_n=b_m\end{array}$.

See süsteem koosneb $m$ lineaarvõrrandist $n$ tundmatuga. Selle võib esitada järgmise maatriksvõrrandina:

$Ax=b$,

kus

$A=\left(\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right);x=\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right);b=\left(\begin{array}{c}{b}_1\\ b_2\\ ⋮\\ b_m\end{array}\right)$+

Maatriks $A$ on lineaarvõrrandisüsteemi koefitsientide maatriks, veeruvektor $x$ on tundmatute vektor ja veeruvektor $b$ on mingi etteantud vektor.

Selleks et süsteemil oleks (vähemalt üks) lahend, on tarvilik ja piisav, et vektor $b$ oleks maatriksi $A$ lineaarkombinatsioon, ja siis vektor $x$ on koefitsientide vektor vektori $b$ lahutuseks maatriksi $A$ veergude järgi.

Maatriksite keeles saab lineaarvõrrandisüsteemi lahenduvuse tingimuse formuleerida Kroneckeri-Capelli teoreemina:

maatriksi $A$ astak võrdub maatriksi $A$ veergudest ja veerust moodustatud $b$ moodustatud maatriksi $[A|b]$ astakuna.

Tähtis erijuht. Kui võrrandite arv langeb kokku tundmatute arvuga ($m=n$ ehk $A$ on ruutmaatriks), siis ühese lahenduvuse tingimus on ekvivalentne maatriksi $A$ pööratavusega.

(Märkus. Süsteemi lahenduvusest ei järeldu veel, et maatriks ei ole kõdunud. Näide: $0x=0$.)

Kui maatriks $A$ on pöötatav, siis süsteemi lahend on

$x=A^{-1}b$.

Sellest tuleneb Crameri meetod.

Lineaarkujutused

Vaatleme lineaarkujutust $𝒜:{ℝ}^n\to {ℝ}^m$ $n$-mõõtmelisest vektorruumist ${ℝ}^n$ $m$-mõõtmelisse vektorruumi ${ℝ}^m$, millel on järgmine kuju:

$\{\begin{array}{ccc}{y}_1& =& a_{11}{x}_1+a_{12}{x}_2+\dots +a_{1n}{x}_n\\ y_2& =& a_{21}{x}_1+a_{22}{x}_2+\dots +a_{2n}{x}_n\\ & \cdots & \\ y_m& =& a_{m1}{x}_1+a_{m2}{x}_2+\dots +a_{mn}{x}_n\end{array}$.

Maatrikskujul on see

$y=Ax$,

kus maatriks $A$ on lineaarkujutuse koefitsientide maatriks.

Kui vaadelda lineaarkujutuse $𝒜$ mõju vektoritele kujul

$e_j=(0,\dots ,0,1_j,0,\dots ,0{)}^T,j=\overline{1,n}$,

mis moodustavad vektorruumi ${ℝ}^n$ baasi, siis $𝒜{𝐞}_j$ on maatriksi $A$ $j$-s veerg.

Niisiis kirjeldab maatriks $A$ lineaarkujutust $𝒜$ täielikult, ja sellepärast nimetatakse seda selle lineaarkujutuse maatriksiks.

Vaata ka

• Regulaarne maatriks
• Ühikmaatriks
• Nullmaatriks
• Skalaarmaatriks
• Diagonaalne maatriks
• Jordani kast
• Kolmnurkmaatriks
• Transponeeritud maatriks
• Sümmeetriline maatriks
• Kaldsümmeetriline maatriks
• Ortogonaalne maatriks
• Kaasmaatriks
• Hermiitiline maatriks
• Antihermiitiline maatriks
• Unitaarne maatriks

Välislingid

Võrgus leiduvad maatriksite kalkulaatorid

• Otsingumootor wolframalpha, mis lahendab mathematica programmeerimiskoodi, sh maatrikseid
• Xiao, Gang Matrix calculator
• Online matrix calculator