Pii

Mall:Pii [pii] ehk Archimedese konstant on matemaatiline konstant, mis on võrdne tasandil paikneva ringjoone pikkuse ja diameetri suhtega (see suhe ei sõltu ringjoone ega diameetri valikust). $\pi$ ligikaudne väärtus on 3,14159.

Seda suurust on tähistatud kreeka tähe $\pi$-ga alates 18. sajandi keskpaigast.

Kuna $\pi$ on irratsionaalarv, siis ei saa seda esitada kahe täisarvu jagatisena (murde, nagu näiteks 22/7, kasutatakse $\pi$ ligikaudsete väärtustena, aga ükski murd ei saa olla selle täpne väärtus). Selle tõttu on $\pi$ kümnendesitus lõpmatu ning samuti ei teki kümnendesituses korduvaid jäädavaid mustreid. Arvatakse, et $\pi$ kümnendesituse numbrid on juhuslikult jaotunud. Lisaks on $\pi$ transtsendentaalne arv ehk arv, mis ei ole ühegi 0-ist erineva ratsionaalarvuliste kordajatega polünoomvõrrandi lahendiks.

Matemaatikud on tuhandeid aastaid püüdnud suurendada oma teadmisi $\pi$-st, arvutades selle väärtust suure täpsusega. Enne 15. sajandit kasutasid matemaatikud, nagu Archimedes ja Liu Hui, geomeetrilisi meetodeid, mis baseerusid hulknurkadel, et hinnata $\pi$ väärtust. Umbes 15. sajandil põhjustasid uued lõpmatutel jadadel põhinevad algoritmid revolutsiooni $\pi$ arvutamises. 20. ja 21. sajandil avastasid matemaatikud ja arvutiteadlased uued lähenemised, mis ühendatuna aina kasvava arvutusvõimsusega võimaldasid hüppeliselt suurendada väljaarvutavate komakohtade arvu. Augustis 2010 anti teada, et $\pi$ väärtusest on kindlaks tehtud 5 triljonit komakohta. Sellega purustati alles sama aasta algul püstitatud varasem rekord, mis oli 2,7 triljonit komakohta. 2011. aastal arvutati üle 10 triljoni $\pi$ komakoha . Teaduslikes arvutustes ei kasutata tavaliselt rohkem kui 40 komakohta. Peamine motivatsioon selliste arvutuste tegemiseks on seega inimkonna soov purustada rekordeid, kuid $\pi$ komakohtade leidmisega seonduvaid mahukaid arvutusi on kasutatud ka superarvutite ja suure täpsusega korrutusalgoritmide võimekuse hindamiseks.

Kuna $\pi$ definitsioon on seotud ringjoonega, siis leidub seda paljudes trigonomeetria ja geomeetria valemites. Eriti nendes, mis on seotud ringide, ellipsite ja sfääridega. Seda esineb ka teistes teadusvaldkondades, nagu näiteks kosmoloogias, arvuteoorias, statistikas, fraktalites, termodünaamikas, mehaanikas ja elektromagnetismis. Kuna $\pi$ esineb nii paljudes teadusharudes, siis on ta ka üks enim tuntud matemaatilisi konstante nii teadlaste kui ka üldise populatsiooni hulgas. $\pi$ kohta on ilmunud mitu raamatut ja tema ülistamiseks peetakse ka Pii päeva. Lisaks jõuavad uued rekordid $\pi$ arvutamisest tihti uudistesse. Samuti võistlevad inimesed $\pi$ komakohtade meelde jätmises. Praegune rekord on üle 67 000 komakoha.

Nimi

Matemaatikud kasutavad ringi ümbermõõdu ja diameetri suhte tähistamiseks kreeka tähte $\pi$. Seda tähte ja sealt tulenevalt ka suurust $\pi$ võib kirjutada ladina sõnaga "pi". Väikest $\pi$-d ei tohi ajada segamine suure $\mathrm{\Pi }$-ga, millega tähistatkse matemaatikas jada liikmete korrutist.

Definitsioon

Animatsioon, mis näitab pii tähendust

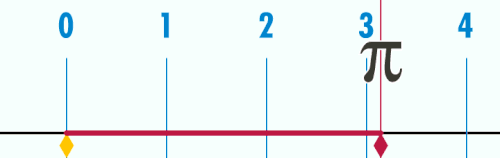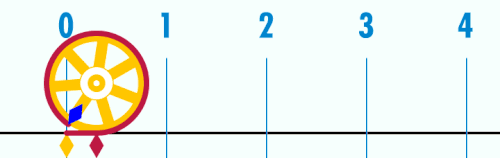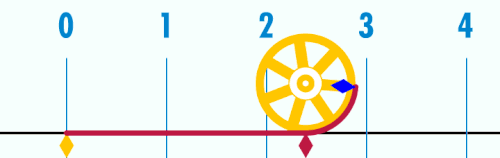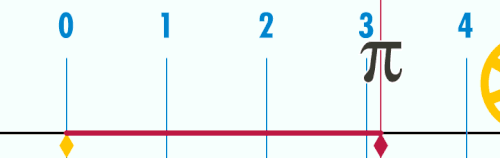
Enamasti on $\pi$ defineeritud kui ringjoone ümbermõõdu suhe tema diameetrisse:

$\pi =\frac{C}{d}$

Suhe C/d on konstant, hoolimata ringjoone suurusest. Näiteks kui ühe ringjoone diameeter on kaks korda pikem kui teise ringjoone diameeter, siis on ka tolle ringjoone ümbermõõt 2 korda suurem, säilitades nii suhte C/d väärtuse. See $\pi$ definitsioon eeldab kaudselt eukleidilist geomeetriat. Ringjoone tähendust saab laiendada ka mitte-eukleidilistesse ruumidesse, aga need uued ringjooned ei rahulda enam võrdust $\pi$=C/d. Eksisteerivad ka teistsugused $\pi$ definitsioonid, mis ei ole seotud ringijoontega. Näiteks on $\pi$ kaks korda suurem vähimast positiivsest x-ist, mille korral cos(x) võrdub nulliga.

Omadused

$\pi$ on irratsionaalarv, mis tähendab, et seda ei saa esitada kahe täisarvu suhtena (murde, nagu näiteks 22/7, kasutatakse $\pi$ ligikaudsete väärtustena, kuid ei leidu ühtegi lõplikku murdu, mis oleks selle täpne väärtus). Kuna $\pi$ on irratsionaalarv, siis on selle kümnendesitus lõpmatu ning kümnendesituses ei teki lõpmatult korduma jäävaid mustreid. $\pi$ irratsionaalsust saab tõestada mitmel moel. Enamik neid mooduseid kasutab diferentsiaal- ja integraalarvutuse meetodeid, tõestades, et vastandjuhul tekiks matemaatiline vastuolu. Veel ei teata, mis täpsuseni saab ratsionaalarvu abil $\pi$ väärtust avaldada, kuid uurimustega on tehtud kindlaks, et see täpsus on suurem kui arvudel e ja ln(2) , kuid väiksem kui Liouville'i numbritel.

$\pi$ on transtsendentne arv, mis tähendab, et see ei ole ühegi ratsionaalarvuliste kordajatega polünoomvõrrandi, nagu näiteks

$\frac{x^5}{120}-\frac{x^3}{6}+x=0$,

lahendiks. $\pi$ transtsendentaalsusest tulenevad kaks järeldust. Esiteks ei saa $\pi$ -d esitada ühegi ratsionaalarvu ja n-astme juure kombinatsioonina. Teiseks, kuna transtsendentaalse arvu pikkust külge ei saa konstrueerida sirge ja kompassi abil, siis ei ole ka võimalik konstrueerida sirge ja kompassi abil ruutu, mille pindala oleks võrdne etteantud ringi pindalaga.

$\pi$ kümnendesituses esinevad numbrid ilma nähtavate mustriteta ja vastavad seniste arvutuste põhjal statistilisele juhuslikkusele. Samuti paistab, et $\pi$ rahuldab normaalsuse testi tingimusi. Lõpmatut arvu nimetatakse normaalseks, kui kõik võrdse suvalise pikkusega numbrikombinatsioonid esinevad sarnase tõenäosusega. $\pi$ normaalsust ei ole suudetud veel tõestada ega ümber lükata. Alates arvutite loomise perioodist on teadlastel olnud teada hulgaliselt $\pi$ komakohtade väärtusi, mida statistiliselt analüüsida. Yasumasa Kanada on uurinud $\pi$-d statistilise analüüsi vaatenurgast ning leidnud, et $\pi$ numbrid vastavad seniste andmete põhjal normaalsuse tingimusele.

Ligikaudne väärtus

Mõned ligikaudsed $\pi$ väärtused:

• murruna: Ligikaudsete murdude hulka kuuluvad kasvava täpsuse järjekorras $\frac{22}{7}$ , $\frac{333}{106}$ , $\frac{355}{113}$ , $\frac{52163}{16604}$ , $\frac{103993}{33102}$
• kümnendsüsteemis: Esimesed sada komakohta on 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679
• kahendsüsteemis: 11.001001000011111101101010100010001000010110100011 ....
• kuueteistkümnendsüsteemis: 3,243F6A8885A308D31319
• kuuekümnendsüsteemis: 3;8,29,44,1
• elliptiliste kõverate ja kompleksarvude korrutamise teooriast tulenev lähendus: $\pi \approx \frac{\ln (640320^3+744)}{\sqrt{163}}$ , mis kehtib umbes 30 komakohani.

Ajalugu

Antiikaeg

Esimesed kirjalikud viited $\pi$ ligikaudsest väärtusest pärinevad Egiptusest ja Babülooniast. Mõlemad hindasid $\pi$ väärtust vähem kui 1% veaga. Babülooniast on leitud ajavahemikust 1900–1600 eKr pärinev savitahvel, millel kasutatakse $\pi$ väärtusena $25/8=3,1250$. Egiptusest on pärit papüürus, mille valmistamise ajaks hinnatakse 1650 eKr ja millel on valem ringi pindala leidmiseks. Seal kasutatakse $\pi$ väärtusena $(16/9{)}^2\approx 3,1605$.

Indiast on leitud aastast 600 eKr pärinevaid viiteid, milles $\pi$ väärtuseks hinnati $(\frac{9785}{5568}{)}^2\approx 3,088$. 150 eKr Indiast pärit leidude põhjal võib öelda, et kasutatud on ka hinnangut $\sqrt{10}\approx 3,1622$.

Hulknurga lähenduse ajastu

Esimene teadaolev algoritm, mille põhjal $\pi$ väärtusi arvutati, põhines geomeetrilisel lähenemisel, kasutades hulknurki. Algoritm seisnes selles ,et ringi sisse konstrueeritakse korrapärane hulknurk, mille tipud toetuvad ringjoonele, ning ringjoonest välja konstrueeritakse korrapärane hulknurk, mille küljed on ringjoone puutujateks. Mida suurem on hulknurkade nurkade arv, seda täpsemalt saab määrata ringjoone pikkuse ja sealt tulenevalt $\pi$ väärtuse.

Selle algoritmi mõtles 250 eKr välja kreeka matemaatik Archimedes ning too meetod valitses ilma eriliste alternatiivideta üle 1000 aasta $\pi$ arvutamise valdkonnas. Hulknurga algoritmiga jõudsid matemaatikud 39 komakoha täpsuseni 1630. aastal. See rekord purustati alles 1699. aastal, kui lõpmatute jadade meetodit kasutades jõuti 71 komakoha täpsuseni.

Lõpmatute jadade ajastu

India matemaatik Madhava (1350–1425) avastas esimesena võimaluse avaldada $\pi$ kuitahes täpne väärtus lõpmatu jada kujul. Kuna aga Euroopasse see avastus ei jõudnud, loetakse lõpmatute jadade abil $\pi$ väärtuse avaldajaks G.W. Leibnitzit ja J. Gregoryt. Lõpmatute jadade uurimise areng 16. ja 17. sajandil põhjustas revolutsiooni $\pi$ arvutamises. Lõpmatud jadad võimaldasid matemaatikutel arvutada $\pi$-d täpsemalt, kui seda olid teinud geomeetrilisi meetodeid kasutanud õpetlased. 1699. aastal arvutas inglise matemaatik Abraham Sharp $\pi$ väärtuse 71 komakoha täpsusega, kasutades Gregory–Leibnizi jada.

$arctan(z)=z-\frac{z^3}{3}+\frac{z^5}{5}-\frac{z^7}{7}+\dots$

See jada on võrdne $\pi$/4, kui arvutada selle väärtus kohal z = 1.

Motivatsioon π arvutamiseks

Enamikus numbrilistes arvutustes, kus kasutatakse $\pi$ väärtust, piisab vähestest komakohtadest, et tagada vajalik täpsus. Jörg Arndti ja Christoph Haeneli järgi läheb enamikus kosmoloogilistes arvutustes vaja 39 komakohta, sest sellise hulga juures saab arvutada nähtava universumi ruumala ühe aatomi ruumala täpsusega. Hoolimata sellest on inimesed näinud suurt vaeva, et arvutada tuhandeid ja miljoneid $\pi$ komakohti. Seda püüet võib osaliselt seletada inimkonna sooviga purustada rekordeid ja sellised saavutused jõuavad sageli uudistesse üle maailma. Samas leidub ka praktilisi põhjuseid. Näiteks hinnatakse sedasi superarvutite võimsust ja numbrilise analüüsi algoritme (kaasa arvatud suure täpsusega korrutamise algoritmid) ning ka matemaatikas kasutatakse saadavat infot $\pi$-s esinevate numbrikombinatsioonide juhuslikkuse uurimiseks.

π arvuteoorias

Arvuteoorias kohtab arvu $\pi$ tihti. Järgnevalt on toodud mõned näited:

• Tõenäosus, et juhuslikult valitud kahe täisarvu suurim ühistegur on üks, on $6/{\pi }^2$. (Tõenäosus on leitud kõigepealt hulga {1,2,3,...,N} jaoks ning mindud seejärel piirile, kus N läheneb lõpmatusele.)
• Tõenäosus, et juhuslikult valitud täisarv ei jagu mõne täisarvu ruuduga, on $6/{\pi }^2$,
• Positiivset täisarvu on võimalik kirjutada kahe täisarvu ruudu summana (järjekord on oluline) keskmiselt $\pi /4$ erineval moel.
• Arvude (1 − 1/p²) korrutis üle algarvude p on $6/{\pi }^2$.Mall:Lisa viide

Kirjandus

• Arndt, Jörg; Haenel, Christoph (2006). Pi Unleashed. Springer-Verlag. ISBN 978-3-540-66572-4. Kasutatud 2013-06-05. ingliskeelne tõlge Catriona ja David Lischka.
• Posamentier, Alfred S.; Lehmann, Ingmar (2004). Pi: A Biography of the World's Most Mysterious Number. Prometheus Books. ISBN 978-1-59102-200-8.
• Eymard, Pierre; Lafon, Jean Pierre (1999). The Number Pi. American Mathematical Society. ISBN 978-0-8218-3246-2., ingliskeelne tõlge Stephen Wilson.

Välislingid

• Wolfram MathWorld, Pi (inglise keeles)
• Esimesed 1 000 000 pii komakohta
• [1] (BBC dokumentaalfilm (inglise keeles), vt 32:00–36:30)