Helilainevõrrand

Helilainevõrrand on füüsikas võrrand, mis kirjeldab helilaine levi keskkonnas. Helilainevõrrand on lainevõrrand ja seega on samuti teist järku osatuletistega diferentsiaalvõrrand. Helilainevõrrand võib kirjeldada helirõhu $p$, osakese kiiruse u, kiiruste potentsiaali $\mathrm{\Phi }$ või siirete potentsiaali $\mathrm{\Psi }$ muutusi sõltuvana asukohast x ja ajast $t$.

Lineaarne homogeenne helilainevõrrand

Lineaarne homogeenne ilma sumbuvuseta helilainevõrrand helirõhust $p$ avaldub kujul:

${\mathrm{\nabla }}^{2}p=\frac{1}{c^2}\frac{{\partial }^{2}p}{\partial t^2}$

kus,

• ${\mathrm{\nabla }}^2$ on Laplace'i operaator;
• $c$ on helikiirus;

Lineaarse homogeense helilainevõrrandi tuletamine

Helilainevõrrandi saab tuletada lineariseeritud olekuvõrrandist, pidevuse võrrandist ja lineariseeritud Newtoni teisest seadusest pideva keskkonna jaoks ehk lineariseeritud Euleri võrrandist.

Akustilised suurused helirõhk ja surutavus

Vaatleme keskkonna ühte osakest. Antud osake hõlmab keskkonna piisavalt suurt ruumala sisaldamaks miljoneid molekule, kuid on piisavalt väike, et tema piires kõik akustilised muutujad (näiteks rõhk, tihedus, osakese siire) on ühtlase suurusega. Antud osakesel on tasakaaluolek ja sellele taskaaluolekule vastab häirimata osakese tihedus

${\rho }_0$

ja häirimata osakese rõhk

${𝒫}_0$

. Osakese piires on rõhk ja tihedus igal ajahetkel sama väärtusega. Helilaine levimisel keskkonnas muutub osakese rõhk ja tihedus ajas. Helilaine levimise ajal leidub osakese piires antud osakese hetkeline tihedus

$\rho$

ja osakesele mõjuv hetkeline rõhk

$𝒫$

. Seejuures on helirõhk on defineeritud hetkelise-

$𝒫$

ja häirimata rõhu

${𝒫}_0$

vahe ehk

$p=𝒫-{𝒫}_0$

.

Akustiline tihedus on analoogselt defineeritud hetkelise tiheduse

$\rho$

ja häirimata tiheduse

${\rho }_0$

vahena. Viimasest olulisema suurusena defineeritakse surutavus

$s$

, mis on akustilise tiheduse ja häirimata tiheduse suhe ehk

$s=\frac{\rho -{\rho }_0}{{\rho }_0}.$

Olekuvõrrand akustikas

Reaalseid gaase ja vedelikke ei saa enamasti lähendada ideaalse gaasiga ja seetõttu määratakse nende puhul mõõtmiste abiga isentroopsed seosed mis esinevad rõhu ja tiheduse muutuste vahel. Viimaseid seoseid saab esitada Taylori reana

$𝒫={𝒫}_0+{\left(\frac{\partial 𝒫}{\partial \rho }\right)}_{{\rho }_0}(\rho -{\rho }_0)+\frac{1}{2}{\left(\frac{{\partial }^2𝒫}{\partial {\rho }^2}\right)}_{{\rho }_0}(\rho -{\rho }_0{)}^2+\dots ,$

kus häirimata oleku voolise isoentroopse kokkusurumise ja paisumise osatuletiste

${\left(\frac{{\partial }^n𝒫}{\partial {\rho }^n}\right)}_{{\rho }_0},n\in 1,2,\dots$

väärtused määratakse katseliselt. Kui häirituse suurus on piisavalt väikese amplituudiga, võib kõrgemat järku Taylori rea liikmed hüljata. Sedasi toimides saame rõhu fluktuatsioonide ja tiheduse muutuste vahel kirja panna lineaarse seose

$𝒫-{𝒫}_0\approx ℬ(\rho -{\rho }_0)/{\rho }_0,$

kus suurust

$ℬ={\rho }_0(\partial 𝒫/\partial \rho {)}_{{\rho }_0}$

, nimetatakse adiabaatiliseks mahtelastsusmooduliks. Kasutades akustilise rõhu ja surutavuse definitsioone saame lineariseeritud olekuvõrrandi kirja panna seosena, mis sarnaneb Hooke'i seadusele ehk

$p\approx ℬs.$

Seega on helirõhk

$p$

ehk hetkeline erinevus tasakaalu oleku rõhust ligikaudu võrdeline surutavusega

$s$

ehk hetkelise tiheduse erinevusega tasakaaluoleku tihedusest ning võrdeteguriks nende kahe suuruse vahel on adiabaatiline mahtelastusmoodul

$ℬ$

.

Keskkonna pidevuse võrrand

Oletades, et vaadeldava osakese ruumala on

$\mathrm{\Omega }$

ja tema pinna pindala

$S$

. Osakese pinna kuju on määratud vektorfunktsiooniga

$d𝐒$

, mis on defineeritav kõikides pinna punktides olevate pinnanormaalide

$𝐧$

ja elementaarpindade

$dS$

korrutisega

$d𝐒=𝐧dS$

. Osakese massi juurdekasv ruumalas

$\mathrm{\Omega }$

võrdub osakese pinda

$S$

läbiva massi voo suurusega:

$\underset{\text{massi muutus}}{\underbrace{\mathrm{\Omega }\frac{\partial \rho }{\partial t}}}=\underset{\text{massi voog läbi pinna}}{\underbrace{-\underset{S}{\int }\rho 𝐮d𝐒}}.$

Kasutades Gauss-Ostrogradski teoreemi, mis seob vektorvälja voo läbi pinna ja pinna sisese tensorvälja

$\underset{S}{\int }(𝐅\cdot 𝐧)dS=\underset{V}{\int }(\mathrm{\nabla }\cdot 𝐅)dV$

saame pidevusvõrrandi parema poole kirjutada kujule

$\underset{S}{\int }\rho 𝐮𝐝𝐒=\underset{\mathrm{\Omega }}{\int }\mathrm{\nabla }(\rho u)d\mathrm{\Omega }.$

Vastavalt eeldustele võib osakese piires osakese kiiruse ja tiheduse korrutise gradienti pidada konstantseks, ning seega võib kirjutada:

$\underset{\mathrm{\Omega }}{\int }\mathrm{\nabla }(\rho u)d\mathrm{\Omega }\approx \mathrm{\nabla }(\rho u)\mathrm{\Omega }.$

Asendades viimase algsesse pidevuse võrrandisse ja jagades mõlemat poolt läbi osakese ruumalaga

$\mathrm{\Omega }$

saame keskkonna pidevuse võrrandi kujul

$\frac{\partial \rho }{\partial t}+\mathrm{\nabla }(\rho u)=0.$

Asendades hetkelise tihedused

$\rho$

surutavusega

$s$

vastavalt tema definitsioonile

$\rho ={\rho }_0+s{\rho }_0$

ja arvestades, et häirimata tihedus

${\rho }_0$

muutub võrreldes surutavusega ajas aeglaselt ja eeldusest tuleneva surutavuse

$s$

vähese muutumisega osakese piires saame lineariseeritud keskkonna pidevuse võrrandi

$\frac{\partial s}{\partial t}+\mathrm{\nabla }u=0.$

Euleri võrrand

Pidevate keskkondade jaoks on Newtoni teine seadus kirja pandav laialt levinust teistsugusel kujul. Pidevas keskkonnas on osakese pinnale mõjuva rõhu resultandi muutus võrdne jõuga, mis paneb osakese massiga

$m=\rho \mathrm{\Omega }$

liikuma vastavalt kiirendusega

$m𝐚=\rho \mathrm{\Omega }𝐚$

ehk

$\underset{\text{inertsijõud}}{\underbrace{\rho \mathrm{\Omega }\frac{D𝐮}{Dt}}}=-\underset{\text{rõhu reslultant}}{\underbrace{\underset{S}{\int }pd𝐒}}.$

Kasutades jälle Gauss-Ostrogradski teoreemi saame Euleri võrrandi parema poole kirjutada

$\underset{S}{\int }pd𝐒=\underset{\mathrm{\Omega }}{\int }\mathrm{\nabla }pd\mathrm{\Omega }.$

Vastavalt eeldustele võib pidevas keskkonnas osakese piires gradienti rõhust lugeda konstantseks ja seega

$\underset{\mathrm{\Omega }}{\int }\mathrm{\nabla }pd\mathrm{\Omega }\approx \mathrm{\nabla }p\mathrm{\Omega },$

mida asendades algsesse Euleri võrrandisse ja jagades mõlemaid pooli ruumalaga

$\mathrm{\Omega }$

saame Euleri võrrandi viia kujule

$\rho \frac{\mathrm{D}𝐮}{\mathrm{D}t}+\mathrm{\nabla }p=0.$

Viimases on

$\mathrm{D}𝐮/\mathrm{D}t$

materiaalne tuletis kiirusest:

$\frac{\mathrm{D}𝐮}{\mathrm{D}t}=\underset{\text{lok. kiirendus}}{\underbrace{\frac{\partial \overrightarrow{u}}{\partial t}}}+\underset{\text{konvektiivne kiirendus}}{\underbrace{u_x\frac{\partial 𝐮}{\partial x}+u_y\frac{\partial 𝐮}{\partial y}+u_z\frac{\partial 𝐮}{\partial z}}}=\frac{\partial 𝐮}{\partial t}+(𝐮\cdot \mathrm{\nabla })𝐮,$

Tavaliselt on helilainete amplituudid väikesed. Olgu

$T$

ja

$L$

helilainele iseloomulikud suurused (harmoonilise laine korral periood ja lainepikkus)

$\frac{\partial }{\partial t}\to \frac{1}{T}\frac{\partial }{\partial x}\to \frac{1}{L}$

$\underset{\text{lokaalne kiirendus}}{\underbrace{\frac{\partial u}{\partial t}\to \frac{u}{T}}}\underset{\text{konvektiivne kiirendus}}{\underbrace{u_x\frac{\partial u}{\partial x}\to \frac{u^2}{L}}}$

$\frac{\text{konvektiivne kiirendus}}{\text{lokaalne kiirendus}}=\frac{u^{2}T}{Lu}=\frac{uT}{L}=\frac{\delta }{L}\ll 1$

Viimases on

$\delta$

osakese siire. Kui osakese siire on lainepikkusega võrreldes väike on konvektiivne kiirendus võrreldes lokaalse kiirendusega samuti väike suurus ja Euleri võrrand lihtsustub kujule

$\rho \frac{\partial \overrightarrow{u}}{\partial t}+\overrightarrow{\mathrm{\nabla }}p=0$

Lineaarse helilainevõrrandi tuletuskäik

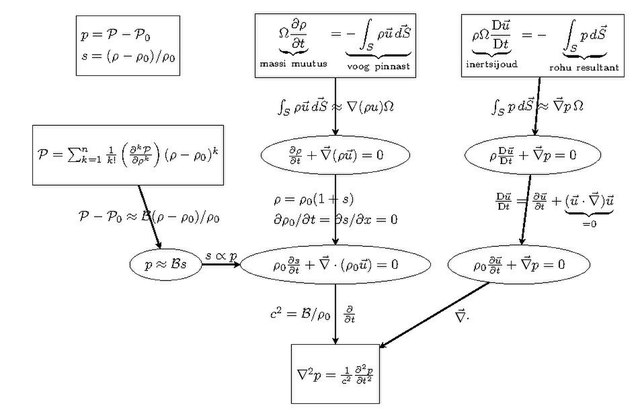
Lineaarne helilainevõrrand

Võttes divergentsi lineaarsest Euleri võrrandist saame

$\mathrm{\nabla }\cdot \left({\rho }_0\frac{\partial 𝐮}{\partial t}\right)=-{\mathrm{\nabla }}^{2}p,$

kus

$\mathrm{\nabla }\cdot \mathrm{\nabla }={\mathrm{\nabla }}^2$

on Laplace'i operaator. Järgnevalt võtame aja järgi tuletise lineaarsest pidevuse võrrandist ja arvestame, et

${\rho }_0$

on ajas vähe muutuv,

${\rho }_0\frac{{\partial }^{2}s}{\partial t^2}+\mathrm{\nabla }\cdot \left({\rho }_0\frac{\partial 𝐮}{\partial t}\right)=0$

lineaarne olekuvõrrand lubab surutavust esitada, kui

$s\approx p/B$

ja kuna

$B$

on ajas vähe muutuv saame

${\mathrm{\nabla }}^{2}p=\frac{1}{c^2}\frac{{\partial }^{2}p}{\partial t^2}$

kus

$c$

on helikiirus, mis on defineeritud kui

$c^2=B/{\rho }_0$

Vaata ka

• Helilaine
• Akustika
• Lainevõrrand