Planetaarülekanne

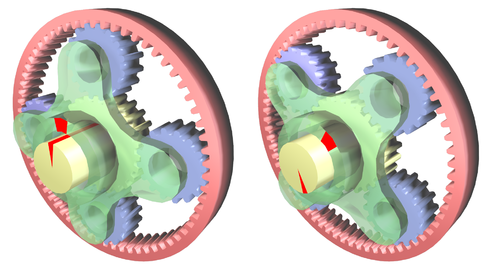
Planetaarülekanne

Planetaarülekandeks nimetatakse hammasülekannet, kus on liikuvate telgedega hammasrattaid. Planetaarülekanded koosnevad välis- ja sisehambumisega hammasratastest. Planetaarülekandes on keskratas välishambumises satelliitidega, mis pöörlevad raami paigutatud telgedel, kusjuures ka raam ise pöörleb. Teisest küljest on satelliidid sisehambumises liikumatu hammasrattaga ning pöörlevad koos raamiga ümber keskratta.

Vedav lüli

Vedavaks lüliks võib planetaarülekandes olla kas keskratas või siis raam. See võimaldab ülekande ühe ja sama skeemi juures saada erinevaid ülekandearve. Lihtsaimal planetaarülekandel, millel on liikumatu ratas ning vedav keskratas võib ülekandearvu leida järgmise valemiga.

$i=\frac{z_{liikumaturatas}}{z_{vedavkeskratas}}+1$

kus

• $z_{liikumaturatas}$ on sisehammastega liikumatu ratta hammaste arv,
• $z_{vedavkeskratas}$ on vedava keskratta hammaste arv.

Kui panna aga pöörlema ka üldjuhul liikumatu sisehammastega ratas, siis sõltub raami nurkkiirus ühtaegu keskmise ja välimise ratta nurkkiirustest ning ülekanne muutub diferentsiaalülekandeks

Planetaarülekande astmete- ja ülekandearv

Planetaarülekanded võivad olla ühe- ja mitmeastmelised ülekandearvuga kuni 1000 ja rohkem.

Planetaarülekande eelised

• Planetaarülekande kasutamine võimaldab vähendada konstruktsiooni massi kahe- ja enamkordselt.
• Satelliitide ühtlane paigutus raamis võimaldab omavahel tasakaalustada planetaarülekandes rataste hambumisel tekkivate jõudude radiaalkomponente.
• Võimaldab saada suuri ülekandearve 1000 ja rohkem.

Planetaarülekande puudused

• Kõrgendatud täpsusnõuded rataste valmistamisel ja koostamisel.
• Madal kasutegur, eriti suurte ülekandearvude korral.

Planetaarülekande konstrueerimisele eelnev arvutus

Planetaarülekannete hammasrattaid arvutatakse tugevusele samade valemitega mis tavaliste ülekannete hammasrattaidki.

Planetaarülekande konstrueerimist alustatakse kinemaatikaarvutustest. Lähtesuurus on nõutav ülekandearv. Kinaemaatikaarvutus seisneb hammasrataste hammaste arvu valikus. Sisselõike vedava keskratta hamba jalal peab tema hammaste arv $z_a$ olema suurem kui 17. Enamasti võetakse $z_a=18$ (kasutatakse ka nihutust ja $z_a\ge 12$). Teiste rataste hammaste arvusid valides arvestatakse kolme tingimust:

• ühistelgsust,
• satelliitide paigutust võrdsete nurkade all (sümmeetrilisust),
• heanaaberlikkust.

Planetaarülekande kinemaatikaarvutus

Planetaarülekande kinemaatikaarvutus tehakse järgmiste valemitega:

• Ülekandesuhe: $i=\frac{{\omega }_a}{{\omega }_h}=1+\frac{z_b}{z_a}$

hammaste arvud z_a≥18; z_b=z_a(i-1); z_g=0,5(z_b-z_a;

• Ühistelgsuse tingimus (kui lähtekontuuri ei nihutata):

$z_b=z_a+2z_g$

• Sümmeetrilisustingimus (koostamistingimus):

$\frac{z_a}{n_{\omega }}=e$ ja $\frac{z_b}{n_{\omega }}=e$ ehk $\frac{z_a+z_b}{n_{\omega }}=e$

kus $n_{\omega }$ on satelliitide arv ülekandes (tavaliselt 3), e aga suvaline täisarv;

• heanaaberikkustingimus:

$a_{\omega }sin\frac{\pi }{n_{\omega }}>0,5d_{satelliidipeaderingjoon}$

,kus $a_{\omega }$ on ülekande telgede vahe, $0,5d_{satelliidipeaderingjoon}$ on satelliidi peaderingjoone läbimõõt.

Pärast kinemaatikaarvutusi tehakse jõuarvutus.

Planetaarülekande jõuarvutus

Planetaarülekande jõuarvutuse esimestes järkudes (materjali ja termotöötluse valik, lubatud pingete määramine) toimitakse üldiselt silinderhammasülekannete arvutamiseks antud soovituste järgi. Erinevused on järgmised:

Lubatud pingete määramisel leitakse eategurid $K_{HL}$ ja $K_{FL}$ rataste suhtelise liikumise järgi, st. $K_{HL}=\sqrt[6]{\frac{N_{HO}}{\acute{N}}}$ ja $K_{FL}=\sqrt[6]{4\frac{10^6}{\acute{N}}}$

, kus $\acute{N}$ on pingevaheldustsüklite arv rataste suhtelisel liikumisel.

• Pingevaheldustsüklite arv vedaval rattal: $\acute{N_a}=573n_{\omega }\acute{{\omega }_a}{L}_h$, kus $\acute{{\omega }_a}={\omega }_{vedav}-{\omega }_{raam}$ on vedava keskratta suhteline nurkkiirus, ${\omega }_{vedav}$ ja ${\omega }_{raam}$ on vedava ratta ja raami nurkkiirused.

Satelliitidel $\acute{N_g}=573\acute{{\omega }_h}{L}_h$, kus $\acute{{\omega }_h}=\frac{{\omega }_{vedav}{z}_a}{z_g}$ on raami suhteline nurkkiirus.

Planetaarülekande telgede vahe

Planetarrülekande telgede vahe määratakse järgmise valemiga:

$a_{\omega }\ge K_a(\acute{i}+1)\sqrt[3]{\frac{\mathrm{\Omega }{K}_{H\beta }{T}_1}{n_{\omega }{\psi }_a\acute{i}[\sigma {]}_H^2}}$

, kus

• $\mathrm{\Omega }=1,1...1,2$ on koormusvoogude ebaühtluse tegur,
• ${\psi }_a$ on hammasratta laiustegur, mis $i\le 6,3$ korral on 0,5 $i>6,3$ korral aga 0,315.
• $\acute{i}=\frac{z_g}{z_a}$

Leitud a_{\omega} väärtus asendatakse lähima suurema väärtusega standardreast.

Suurratta laius planetaarülekandes

Suurratta laius planetaarülekandes arvutatakse valemiga $b_2={\psi }_a{a}_{\omega }$

Väikeratta läbimõõt

$d_1=\frac{2a_{\omega }}{i+1}$

Ülekande moodul

$m=\frac{d_1}{z_a}$

Arvutatud mooduli väärtus asendatakse lähima väärtusega standardreast Pärast seda määratakse hammasrataste läbimõõdud, selgitatakse toorikute sobivus ja arvutatakse hambumisjõud.

Hammasrataste toorikute sobivus planetaarülekandes

Et termotöötlusega saada arvutamisel eeldatud hammasrataste mehaanilisi omadusi, ei tohi toorikud olla lubatust suuremad.

Ringjõud

$F_t=\frac{2\mathrm{\Omega }{T}_1}{n_{\omega }{d}_1}$

Seejärel kontrollitakse painde- ja kontaktpingeid.

Planetaarülekande konstrueerimine

Arvutustele järgneb konstrueerimine. Nagu tavalisegi reduktori korral, koostatakse algul eskiisprojekt.

Planetaarülekande eskiisprojekt

Eskiisprojekti korral planetaarülekandes määratakse:

• detailide põhimõõtmed ja vastastikune asend,
• võllide esialgsed mõõtmed,
• detailide vahekaugused,
• detailide toereaktsioonid,
• valitakse laagrite tüübid ning mõõtmed. Keskrataste võllid toetatakse kerge seeria radiaalkuullagritele, satelliidid aga keskmise seeria sfäärilistele kuul- või rulllaagritele.

Saadud tulemuste põhjal tehakse esialgne eskiisprojekt koos esialgsete eskiisjoonistega.

Planetaarülekande projekt

Planetaarülekande lõpliku projekti tegemisel võetakse arvesse kõiki eelnevalt arvutustega leitud tulemusi ning lisaks eelnevatele arvutustele tehakse veel järgnevat.Valitud veerelaagritele tehakse kontrollarvutus toereaktsioonidega, mis leitud jooniselt. Arvestades suurimat võimalikku pöördemomenti jaotuse ebaühtlust voogude vahel, määratakse see jõud kiirel(vedaval) võllil $F=\frac{0,4T_1}{d_1}$, kus d₁ on hammassiduri jaotusläbimõõt. Aeglasel vedaval võllil $F=\frac{0,2T_h}{a_{\omega }}$, kus T_h on moment väljundvõllil (raamil), a_ω ülekande telgede vahe. Kõige rohkem ongi koormatud satelliitide laagrid. Nende vajalik dünaamiline kandevõime C_vajalik leitakse jõu $F_r=2F_t$ järgi, kus $F_t$ on eelnevalt arvutataud ringjõud.

Vaata ka

• hammasülekanne
• hammasratas