Lõplike elementide meetod

Lõplike elementide meetod ehk LEM (ingl k finite element method, FEM) on numbriline arvutusmeetod insener-tehniliste ja füüsikaliste probleemide lahendamiseks. Meetod hõlmab üldiste (osatuletistega) diferentsiaalvõrrandite ja/või nende süsteemi aproksimeerimist ehk lähendamist üle mingi (pideva) piirkonna (nt tasand), mis jaotatakse väiksemateks, lõplikeks elementideks (nn piirkonna diskreetimine). Numbriline lahend kogu piirkonna jaoks saadakse lõplike elementide summeerimisega mingi eeskirja järgi.

Ajalugu

Esmakordselt kasutas piirkonna diskreetimist saksa matemaatik Karl Schellbach 1851. aastal, seda Plateau probleemi lahendamisel. Lord Rayleigh', Walther Ritzi ja Boris Galjorkini hilisem arendustöö variatsiooniarvutuse ja kaalutud hälvete meetodites andis samuti märkimisväärse panuse LEMi teooriasse. Hiljem on diskreetimist kasutanud Richard Courant, kes 1943. aastal uuris Saint-Venant' väändeprobleemi, kasutades ka Rayleigh'-Ritzi meetodit, kuigi tema töö jäi suurema tähelepanuta. Kaasaegse LEMi formuleerimisele aitas kaasa John Argyrise 1954. aastal avaldatud artikkel struktuurianalüüsi ja energiateoreemi teemadel. Argyrisest sõltumatult panustasid tänapäevase LEMi väljatöötamisse Ray William Clough (1960) ja M. J. Turner (1956), kellest viimane võttis kasutusele termini lõplik element. Seoses aeronautikatööstuse ja arvutusjõudluse arenguga 1960. aastatel arendas NASA välja esimese LEMi tarkvara NASTRAN struktuurianalüüsi arvutuste jaoks. Edasistel aastatel kujunes LEM tööstusstandardiks, laienedes esialgsest struktuurianalüüsist soojusjuhtivuse, hüdromehaanika ja elektrodünaamika simulatsioonideni. Personaalarvutite tulekuga 1970. aastate lõpus ilmusid turule esimesed LEMi kommertstarkvarapaketid.

Meetodi põhimõte

Lõplike elementide 2D-võrgustik

LEMi 2D-lahend

Üldjoontes viiakse LEM läbi järgnevalt:

1. määratakse probleemi dimensionaalsus, vastavad võrrandid, nende kehtivus- ja määramispiirkonnad (defineerib elementide dimensionaalsuse);
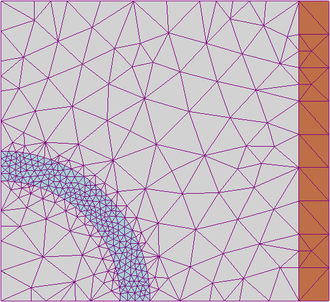
2. piirkond jaotatakse väiksemateks osadeks e lõplikeks elementideks (kolmnurk, ristkülik jne) e diskreeditakse, st koostatakse lõplike elementide võre (ingl k mesh), milles iga element on seotud teise elemendiga võre sõlmpunkti kaudu (vt parempoolset joonist); piirkonna lihtsamateks osadeks jaotamisel on mitu eelist:
   • keeruka geomeetria täpne kirjeldus;
   • erinevate materjaliomaduste arvestamine;
   • lokaalsete efektide arvestamine.
3. iga element, täpsemini võre sõlmpunkt, seostatakse
   • vabadusastmete arvuga (määrab elemendi edasise käitumise);
   • materjali, üldiselt välja omadustega (termodünaamilistes simulatsioonides nt soojusmahtuvusega);
   • asjakohaste (füüsikaliste) harilike diferentsiaal- või algebraliste võrranditega (eeldatakse, et sõltumatud muutujad võre sõlmpunktides on teada või siis need aproksimeeritakse mingi polünoomi abil);
4. kõikide elementide panused summeeritakse, saades kogu probleemi kirjeldava globaalse võrrandite süsteemi;
5. saadud võrrandite süsteem lahendatakse numbriliselt (vaja algväärtusi, nt temperatuurijaotus);
6. vajalikud füüsikalised suurused arvutatakse iga elemendi jaoks.

Ülaltoodud punktidest järeldub, et LEM sobib mittelineaarsete efektide uurimiseks. Samuti nähtub punktidest, et vaadeldav pidev süsteem lõpmatu arvu tundmatutega lähendatakse diskreetse süsteemi ja lõpliku arvu tundmatutega. Kui teatud piirkonnas vajatakse suuremat täpsust, siis seal saab konstrueerida tihedama elementide võrgustiku. Tegemist oleks optimaalse lahendusega, kuna kogu piirkonda pole mõtet väga tihedalt diskreetida: nõudmised arvuti muutmälu, salvestusseadmete ja protsessorijõudluse osas kasvaksid viimasel juhul drastiliselt.

Probleeminäide

LEMi tehniliseks käsitluseks sobib ühedimensiooniline homogeenne Dirichlet' probleem

(1):$u^{″}(x)=f(x),x\in (0,1),u(0)=u(1)=0,$

kus $f(x)$ on teadaolev funktsioon ja $u(x)$ otsitav lahend. Esmalt tuleb formuleerida ääreväärtusprobleemi nõrk formulatsioon e nõrk vorm, seejärel see diskreetida.

Korrutades esimest võrrandit valemis (1) skalaarselt suvalise funktsiooniga $v(x)$, mis rahuldab

(2):$v(0)=v(1)=0,$

saadakse

(3):$\underset{0}{\overset{1}{\int }}v(x)u^{″}(x)dx=\underset{0}{\overset{1}{\int }}v(x)f(x)dx.$

Võrrandi vasaku poole ositi integreerimine annab

$\underset{0}{\overset{1}{\int }}v(x)u^{″}(x)dx=v(x)u^{\prime }(x){|}_0^1-\underset{0}{\overset{1}{\int }}{v}^{\prime }(x)u^{\prime }(x)dx=-\underset{0}{\overset{1}{\int }}{v}^{\prime }(x)u^{\prime }(x)dx,$

milles viimase võrduse saamiseks kasutati valemit (2). Defineerides funktsionaali $\varphi (u,\cdot )$ järgnevalt:

$\varphi (u,v)=\underset{0}{\overset{1}{\int }}{u}^{\prime }(x)v^{\prime }(x)dx,$

saab valemi (3) kirja panna kui

(4):$\underset{0}{\overset{1}{\int }}v(x)f(x)dx=-\varphi (u,v).$

Tegemist on nõrga vormiga probleemi (1) jaoks selles mõttes, et see seab nõrgemad tingimused lahendile $u$ ja proovifunktsioonile $v$. Kui ääreväärtusprobleem oleks defineeritud üle mingi suvalise piirkonna $\mathrm{\Omega }$, siis vastavad testfunktsioonid moodustaksid Sobolevi ruumi $H^1(\mathrm{\Omega })$. Testfunktsioonid rahuldavad $v{|}_{\mathrm{\Gamma }}=0$, kus $\mathrm{\Gamma }$ on piirkonna $\mathrm{\Omega }$ tükati sile raja. On võimalik näidata, et $u\in H^1(\mathrm{\Omega })$. Probleeminäite testfunktsioonide ruumiks on $H^1(0,1)$.

Diskreetimine

Nõrga vormi (4) diskreetimine taandub lõpmatu-dimensioonilise lineaarse probleemi

$\text{ leia }u\in H^1(0,1)\text{ nii, et }\mathrm{\forall }v\in H^1(0,1)\text{ korral }-\varphi (u,v)=\int fv$

asendamisele lõpliku-dimensioonilise probleemiga

(5):$\text{ leia }u\in V\subset H^1(0,1)\text{ nii, et }\mathrm{\forall }v\in V\text{ korral }-\varphi (u,v)=\int fv$

kus $V$ on lõpliku dimensiooniga tükiti polünoomide ruum.

Võttes intervalli $(0,1)$, jagatakse see $n+1$ osaks: $0=x_0<x_1<\dots <x_n<x_{n+1}=1$. Ruumi $V$ määratletakse kui

(6):$V=\{v:[0,1]\to ℝ|v\in C^0,v{|}_{[x_k,x_{k+1}]}\text{ on lineaarne }\mathrm{\forall }k=0,\dots ,n\text{ ja }v(x_0)=v(x_{n+1})=0\},$

milles $C^0$ tähistab pidevate funktsioonide hulka. Ülaltoodud definitsiooni kohaselt pole $v$ diferentseeruv kogu määramispiirkonna ulatuses, st punktides $\{x_k{\}}_{k=0}^{n+1}$ funktsiooni $v$ tuletist ei leidu.

Baasi valik

Baasifunktsioonid v_k (sinised) ning lineaarkombinatsioon neist (punane)

Ruumi $V$ jaoks saab valida järgneva baasi:

$v_k(x)=\{\begin{array}{cc}\frac{x-x_{k-1}}{x_k-x_{k-1}},& \text{ kui }x\in [x_{k-1},x_k],\\ \frac{x_{k+1}-x}{x_{k+1}-x_k},& \text{ kui }x\in [x_k,x_{k+1}],\mathrm{\forall }k=1,\dots ,n\\ 0& \text{ muul juhul }\end{array}.$

Sellise definitsiooni kohaselt on igas intervallis $[x_{k-1},x_{k+1}]$ defineeritud baasifunktsioon $v_k$ kolmnurkfunktsioon. Kehtib $v_i(x_j)={\delta }_{ij}$, kus ${\delta }_{mn}$ tähistab Kroneckeri sümbolit. Baas rahuldab järgmisi omadusi:

(7):$\underset{0}{\overset{1}{\int }}{v}_j{v}_{k}dx=0,\varphi (v_j,v_k)=0,\text{ kui kehtib }|j-k|>1.$

Maatriksi kujule viimine

Kirjutades otsitava funktsiooni $u(x)$ baasifunktsioonide $v_k(x)$ kaudu

$u(x)=\sum _{k=1}^n{u}_k{v}_k(x)$

ja tähistades valemis $v(x)=v_j(x)$, saab valemi (5) kirja panna kui

(8):$-\sum _{k=1}^n{u}_k\varphi (v_k,v_j)=\sum _{k=1}^n\int f(x)v_k(x)dx,\mathrm{\forall }j=1,\dots ,n.$

Defineerides vektorid $𝐮=(u_1,\dots ,u_n{)}^T$ ja $𝐛=(b_1,\dots ,b_n{)}^T$, kus $b_i=\int f(x)v_i(x)dx$, ning maatriksi $L=L_{ij}=\varphi (v_i,v_j)$, saab valemi (8) avaldada kui

(9):$-L𝐮=𝐛.$

Järelikult on ääreväärtusprobleem taandunud $𝐮$ leidmisele võrrandis (9). Omaduse (7) tõttu on maatriks $L$ sümmeetriline, positiivselt määratud ja hõre, st enamus tema elementidest on nullid. Seda tüüpi võrrandite jaoks on välja töötatud mitmesuguseid algoritme, näiteks konjugeeritud gradiendi meetod ning LU- ja Cholesky dekompositsioon, mis arvutite peal efektiivselt realiseeruvad.

Üldistused

LEMi on võimalik rakendada ka kõrgemaid (osa)tuletisi sisaldavatele ääreväärtusprobleemidele, näiteks Neumanni ja segaprobleemile, üle suvalise piirkonna $\mathrm{\Omega }$. Diferentsiaalvõrrandi järk määrab baasifunktsioonide pidevuse tingimused, piirkonna dimensionaalsus aga elementide dimensiooni, näiteks $\mathrm{\Omega }\subset {ℝ}^2$ võib jaotada kolmnurkadeks, ruutudeks või muuks kumeraks hulknurgaks, $\mathrm{\Omega }\subset {ℝ}^3$ tetraeedriteks jne (ühedimensioonilises probleeminäites on piirkond sirglõikudeks jaotatud). Nõrk vorm formuleeritakse Greeni identsusi kasutades, nt homogeense Dirichlet' probleemi nõrgaks vormiks on

$\underset{\mathrm{\Omega }}{\int }fvdV=-\underset{\mathrm{\Omega }}{\int }\mathrm{\nabla }u\cdot \mathrm{\nabla }vdV=-\varphi (u,v).$

Baasifunktsioonid e interpolatsioonifunktsioonid on üldjuhul tükati polünoomid, nt Hermite'i ja Lagrange'i polünoomid, kusjuures nende väärtused peavad pidevuse tagamiseks erinevate elementide kokkupuuteäärel olema võrdsed. Nõrga vormi koostamist ja selle lähendamist lõpliku baasiga nimetatakse Galjorkini meetodiks. Ülesanne taandub lõpuks numbrilisele maatriksivõrrandi lahendamisele või Runge-Kutta meetodi rakendamisele.

Võrdlus lõplike vahede meetodiga

Lõplike vahede meetod (LVM) on alternatiivne viis osatuletistega diferentsiaalvõrrandite (süsteemi) lahendamiseks. Põhilised erinevused LEMi ja LVMi vahel on:

• LEM suudab keeruka geomeetria ja ääreväärtusprobleemi lahendada, samas kui LVMi lahendamise piirkond on ristkülikukujuline (või ristkülikutest koosnev);
• LVMi on lihtsam implementeerida;
• LVM on teatud probleemide (nt Poissoni võrrandi) puhul LEMi erijuht;
• LEMi lähendus on üldjuhul täpsem vastavast LVMi omast (kuigi see sõltub üsna palju probleemi püstitusest; LVMiga sama täpsuse saavutamiseks vajab LEM palju vähem võre sõlmpunkte, järelikult implementeerimisel ka vähem mälu andmete töötlemiseks).

LEMi kasutatakse üldiselt struktuurianalüüsis, samas kui arvutuslikus hüdrodünaamikas (nt õhuvoolude simulatsioon lennukitiiva ümber) kasutatakse rohkem LVMi või lõpliku ruumala meetodit.

Rakendused

LEM on populaarne mehaanika valdkonda kuuluvate insener-tehniliste probleemide simulatsioonides. LEM on integreeritud aeronautika-, ehitus-, laeva-, auto- ja isegi mööblitööstuse disainimis- ning tootmisprotsessi. Paljud LEMi tarkvarapaketid koosnevad komponentidest, millest igaüks käsitleb erinevaid füüsikavaldkondi, nt termodünaamika, elektromagnetism, hüdrodünaamika ja mehaanika. LEM aitab visualiseerida materjalide pingeid, nende jaotust ja konstruktsiooni vastupidavust, samuti on võimalik minimeerida erinevaid karakteristikuid, näiteks kaalu, materjali- ja tootmiskulu. LEMi tarkvara võimaldab simulatsiooni parametriseerida (nt konstruktsiooni pingete simulatsioon, kus parameetriks on erineva raskusega koormised), arvestada ajalist sõltuvust ja saada tulemus soovitud täpsuse piires.

LEM on märkimisväärselt parandanud tootearenduse standardeid ja metodoloogiat, seda eriti tööstusvaldkonnas. Näiteks on LEMi kasutuselevõtuga kontseptsioonist tootmisliinini jõudmise aeg oluliselt vähenenud. Seda tänu prototüüpide tarkvaralise testimise võimalusele, mis elimineerib mitteoptimaalsed või -töötavad prototüübid ning nendega seotud kulud, näiteks materjal ja aeg, tootearenduse algetappides.

Lisaks tööstuslikule rakendusele uuritakse LEMi abil füüsikalisi olukordi, mille tingimustes on raske eksperimenti läbi viia või seda seletav mudel vajaks kontrollimist.

Vaata ka

• Galjorkini meetod
• Kompuuterfüüsika
• Lõplike vahede meetod
• Numbrilised meetodid
• Rayleigh'-Ritzi meetod
• Variatsiooniarvutus

Kirjandus

Eesti keeles

• Lahe, Andres. Lõplike elementide meetod. Tallinn, 2008. [1]
• Kirs, Jüri. Sissejuhatus lõplike elementide meetodisse (I,II,III osa). Tallinn, 2001.
• Kasemägi, Heiki. Kompuuterfüüsika II. Tartu, 2009.

Võõrkeeltes

• Ottosen, N.S.; Petersson, H. Introduction to the Finite Element Method. Prentice Hall, 1992. ISBN 978-0134738772
• Zienkiewicz, O.C; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals (6th ed). Butterworth-Heinemann, 2006. ISBN 978-0750663205
• Segerlind, L.J. Applied Finite Element Analysis (2nd ed). John Wiley & Sons, 1984. ISBN 978-0-471-80662-2
• Lewis, R.W.; Nithiarasu, P.; Seetharamu, K. Fundamentals of the Finite Element Method for Heat and Fluid Flow. John Wiley & Sons, 2004. ISBN 978-0470847893

Välislingid

• Scholarpedia – Finite element method