Kvant-masinõpe

Kvant-masinõpe on kvantalgoritmide integreerimine masinõppeprogrammidesse.

Mõiste kõige levinum kasutusviis viitab masinõppe algoritmidele klassikaliste andmete analüüsimiseks, mida teostatakse kvantarvutis, st kvant-täiustatud masinõppes. Kui masinõppe algoritme kasutatakse tohutute andmemahtude arvutamiseks, siis kvant-masinõpe kasutab kvantbitte ja kvantoperatsioone või spetsiaalseid kvantsüsteeme, et parandada programmi algoritmide arvutuskiirust ja andmete salvestamist. See hõlmab hübriidmeetodeid, mis sisaldavad nii klassikalist kui ka kvanttöötlust, kus arvutuslikult keerulised alamprogrammid suunatakse kvantseadmesse. Need tööd võivad olla olemuselt keerukamad ja kvantarvutis kiiremini täidetavad. Lisaks saab kvantalgoritme kasutada kvantolekute analüüsimiseks klassikaliste andmete asemel.

Lisaks kvantarvutitele seostatakse mõistet "kvant-masinõpe" ka klassikaliste masinõppemeetoditega, mida rakendatakse kvantkatsetest (st masinõpe kvantsüsteemidest) genereeritud andmetel, näiteks kvantsüsteemi faasisiirete õppimises või uute kvantkatsete loomises.

Kvant-masinõpe laieneb ka teadusharru, mis uurib metodoloogilisi ja struktuurilisi sarnasusi teatud füüsiliste süsteemide ja õppesüsteemide, eelkõige närvivõrkude vahel. Näiteks on mõned kvantfüüsika matemaatilised ja numbrilised tehnikad rakendatavad klassikalises süvaõppes ja vastupidi.

Lisaks uurivad teadlased õppeteooria abstraktsemaid mõisteid seoses kvantinformatsiooniga, mida mõnikord nimetatakse "kvantõppe teooriaks".

Neli erinevat lähenemisviisi kvantarvutite ja masinõppe distsipliinide ühendamiseks. Esimene täht viitab sellele, kas uuritav süsteem on klassikaline (C) või kvant (Q), teine täht aga määrab, kas kasutatakse klassikalist või kvantinfotöötlusseadet.

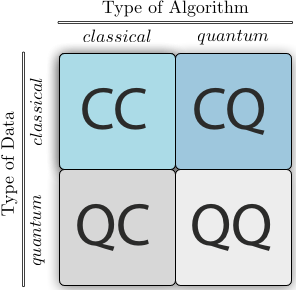
Masinõpe kvantarvutitega

Kvant-täiustatud masinõpe viitab kvantalgoritmidele, mis lahendavad masinõppe ülesandeid, parandades ja sageli kiirendades klassikalisi masinõppe tehnikaid. Sellised algoritmid nõuavad tavaliselt antud klassikalise andmestiku kodeerimist kvantarvutisse, et muuta see kvantteabe töötlemiseks kättesaadavaks. Seejärel rakendatakse kvantteabe töötlemise rutiine ja kvantarvutuse tulemus loetakse kvantsüsteemi mõõtmise teel ette. Näiteks on kvantbiti mõõtmise tulemus samaväärne binaarse klassifitseerimisülesande tulemusega. Kuigi paljud kvant-masinõppe algoritmide ettepanekud on endiselt puhtalt teoreetilised ja nõuavad täismahus universaalse kvantarvuti testimist, on teisi algoritme rakendatud väikesemahulistes või eriotstarbelistes kvantseadmetes.

Kvant-assotsiatiivsed mälud ja kvantmustrite tuvastamine

Assotsiatiivsed mälud (ehk sisu-aadressiga mälud) suudavad tuvastada salvestatud sisu, lähtudes selle sarnasuse mõõtmisest, mitte fikseeritud aadressidest, nagu muutmäludes. Seetõttu peavad nad suutma taastada nii mittetäielikke kui ka rikutud mustreid, kuna mustrituvastus on masinõppe oluline ülesanne.

Tüüpilised klassikalised assotsiatiivmälud talletavad p mustrit $O(n^2)$ interaktsioonides (sünapsides), mis paiknevad võrgu n tehisneuronite vahel reaalsetes sümmeetrilistes energiamaatriksites. Kodeerimine on tehtud nii, et soovitud mustrid vastavad energiafunktsionaali lokaalsetele miinimumidele. Mustrite taastamine toimub, vähendades süsteemi kogutud energiat, alustades algsest konfiguratsioonist.

Kahjuks on klassikaliste assotsiatiivmälude võime piiratud ülekostvuse nähtusega. Kui salvestatakse liiga palju mustreid, tekivad eksimused, mis levivad kiiresti, põhjustades energia maastiku korratust ja muutes mustrite taastamise võimatuks. Salvestatavate mustrite arv on tavaliselt piiratud neuronite arvu lineaarse funktsiooniga, $p\le O(n)$ .

Kvant-assotsiatiivsed mälud (oma lihtsaimas teostuses) salvestavad mustrid unitaarmaatriksisse $U$, mis toimib n kvantbitist koosnevas Hilberti ruumis. Mustrite otsimine toimub, viies algse oleku unitaarse evolutsiooni abil superpositsiooni soovitud mustritega, kus tõenäosusjaotus on tipnenud sisendile kõige sarnasema mustri juures. Oma omaduste poolest on otsinguprotsess seega tõenäosuslik.

Kuna kvantassotsiatiivsed mäludes ei esine ülekostvust, ei teki neil kunagi vigaseid salvestusi. Vastavalt sellele on nende mahtuvus klassikalistest assotsiatiivmälu tüüpidest suurem. Unitaarmaatriksil $O(pn)$ parameetrit, mistõttu on võimalik realiseerida efektiivseid ja eksimustest vabu kvant-assotsiatiivseid mälusid, mis suudavad käsitleda mistahes polünoomset arvu mustreid.

Kvantbinaarne klassifikaator

Mustrikorraldus on masinõppe üks olulisi ülesandeid ning binaarne klassifikatsioon on üks tööriistu mustrite leidmiseks. Binaarset klassifikatsiooni kasutatakse juhendatud masinõppes ja juhendamata masinõppes. Kvant-masinõppes teisendatakse klassikalised bitid kvantbittideks ja kaardistatakse Hilberti ruumi; kvantbinaarne klassifikaator kasutab keerukate väärtustega andmeid, et ära kasutada Hilberti ruumi eeliseid. Kasutades ära kvantmehaanika omadusi, nagu superpositsioon, põimumine, interferents, annab kvantbinaarne klassifikaator lühikese aja jooksul täpseeid tulemusi.

Klassikaline õpe, mida rakendatakse kvantprobleemide lahendamiseks

Mõiste "kvant-masinõpe" viitab mõnikord klassikalisele masinõppele, mida tehakse kvantsüsteemidest saadud andmete põhjal. Selle lihtne näide on kvantoleku tomograafia (Inglise Quantum state tomography), kus kvantolekut õpitakse mõõtmise teel. Muude rakenduste hulka kuuluvad ka Hamiltonlaste õppimine ja kvantkatsete automaatne genereerimine.

Skeptilisus

Masinõpe ei ole praegu mitte ainult uurimisvaldkond, vaid ka majanduslikult oluline ja kiiresti kasvav tööstusharu ning kvantarvuti on nii teoreetilise kui ka eksperimentaalse uurimistöö väljakujunenud valdkond, siis kvant-masinõpe jääb puhtalt teoreetiliseks õppevaldkonnaks. Katsed eksperimentaalselt demonstreerida kvant-masinõppe kontseptsioone on endiselt ebapiisavad. Lisaks on ennustamise etapis veel üks takistus, kuna kvantõppemudelite väljundid on oma olemuselt juhuslikud. See tekitab sageli märkimisväärseid kulusid, kuna tegeliku prognoosi saamiseks tuleb paljud kvantõppemudeli käitamised agregeerida.

Paljud juhtivad teadlased, kes panustavad laialdaselt kvant-masinõppe valdkonda, hoiatavad selle teema laiaulatusliku reklaami eest ja on väga vaoshoitud, kui neilt küsitakse selle praktilise kasutamise kohta lähitulevikus. Sophia Chen kogus kokku mõned selle valdkonna tuntud teadlaste väited:

• "Ma arvan, et me pole veel oma kodutööd teinud. See on äärmiselt uus teadusvaldkond," - füüsik Maria Schuld Kanadas asuvast kvantarvutite idufirmast Xanadu.
• "Kui segate masinõpet kvantmehaanikaga, soositete liigselt elevust." – Jacob Biamonte, kvantarvutuste teooriasse panustaja.
• "Selleks, et väita, et kvant-masinõpe tegelikult töötab, tuleb teha palju rohkem tööd," - arvutiteadlane Iordanis Kerenidis, Silicon Valleys asuva kvantarvutite startupi QC Ware juht.
• "Ma ei ole näinud ühtegi tõendit selle kohta, et on olemas mõtestatud [masinõppe] ülesanne, mille jaoks oleks mõttekas kasutada kvantarvutit, mitte klassikalist arvutit," - füüsik Ryan Sweke Berliini vabaülikoolist Saksamaal.

Vaata ka

• Diferentseeritav programmeerimine
• Kvantarvutus
• Lineaarsete võrrandisüsteemide kvantalgoritm
• Kvantlõõmutamine
• Kvantnärvivõrk
• Kvantkujutis