Fail:Fourier transform, Fourier series, DTFT, DFT.gif
Allikas: testwiki
Mine navigeerimisribale
Mine otsikasti

Selle eelvaate suurus: 800 × 477 pikslit. Teised eraldusvõimed: 320 × 191 pikslit | 640 × 381 pikslit | 1128 × 672 pikslit.
Algfail (1128 × 672 pikslit, faili suurus: 59 KB, MIME tüüp: image/gif)
See on jagatud fail allikast Wikimedia Commons ja seda saab kasutada ka teistes projektides. Faili sealne kirjeldus on kuvatud allpool.
Lühikirjeldus
| KirjeldusFourier transform, Fourier series, DTFT, DFT.gif |
English: A Fourier transform and 3 variations caused by periodic sampling (at interval T) and/or periodic summation (at interval P) of the underlying time-domain function. |
|||
| Kuupäev | ||||
| Allikas | Üleslaadija oma töö | |||
| Autor | Bob K | |||
| Luba (Faili edasikasutus) |
Autoriõiguse omanikuna avaldan selle teose järgmise litsentsi all:
|
|||
| Teised versioonid |
File:Variations_of_the_Fourier_transform.tif, Derivative works of this file: Fourier transform, Fourier series, DTFT, DFT.svg,
|
|||
| GIF genesis InfoField | ||||
| Octave/gnuplot source InfoField | click to expand
This graphic was created with the help of the following Octave script: pkg load signal
graphics_toolkit gnuplot
%=======================================================
% Consider the Gaussian function e^{-B (nT)^2}, where B is proportional to bandwidth.
T = 1;
% Choose a relatively small bandwidth, so that one cycle of the DTFT approximates a true Fourier transform.
B = 0.1;
N = 1024;
t = T*(-N/2 : N/2-1); % 1xN
y = exp(-B*t.^2); % 1xN
% The DTFT has a periodicity of 1/T=1. Sample it at intervals of 1/8N, and compute one full cycle.
% Y = fftshift(abs(fft([y zeros(1,7*N)])));
% Or do it this way, for comparison with the sequel:
X = [-4*N:4*N-1]; % 1x8N
xlimits = [min(X) max(X)];
f = X/(8*N);
W = exp(-j*2*pi * t' * f); % Nx1 × 1x8N = Nx8N
Y = abs(y * W); % 1xN × Nx8N = 1x8N
% Y(1) = SUM(n=1,2,...,N): { e^(-B × t(n)^2) × e^(-j2π ×-4096/8N × t(n)) }
% Y(2) = SUM(n=1,2,...,N): { e^(-B × t(n)^2) × e^(-j2π ×-4095/8N × t(n)) }
% Y(8N) = SUM(n=1,2,...,N): { e^(-B × t(n)^2) × e^(-j2π × 4095/8N × t(n)) }
Y = Y/max(Y);
% Resample the function to reduce the DTFT periodicity from 1 to 3/8.
T = 8/3;
t = T*(-N/2 : N/2-1); % 1xN
z = exp(-B*t.^2); % 1xN
% Resample the DTFT.
W = exp(-j*2*pi * t' * f); % Nx1 × 1x8N = Nx8N
Z = abs(z * W); % 1xN × Nx8N = 1x8N
Z = Z/max(Z);
%=======================================================
hfig = figure("position", [1 1 1200 900]);
x1 = .08; % left margin for annotation
x2 = .02; % right margin
dx = .05; % whitespace between plots
y1 = .08; % bottom margin
y2 = .08; % top margin
dy = .12; % vertical space between rows
height = (1-y1-y2-dy)/2; % space allocated for each of 2 rows
width = (1-x1-dx-x2)/2; % space allocated for each of 2 columns
x_origin1 = x1;
y_origin1 = 1 -y2 -height; % position of top row
y_origin2 = y_origin1 -dy -height;
x_origin2 = x_origin1 +dx +width;
%=======================================================
% Plot the Fourier transform, S(f)
subplot("position",[x_origin1 y_origin1 width height])
area(X, Y, "FaceColor", [0 .4 .6])
xlim(xlimits);
ylim([0 1.05]);
set(gca,"XTick", [0])
set(gca,"YTick", [])
ylabel("amplitude")
%xlabel("frequency")
%=======================================================
% Plot the DTFT
subplot("position",[x_origin1 y_origin2 width height])
area(X, Z, "FaceColor", [0 .4 .6])
xlim(xlimits);
ylim([0 1.05]);
set(gca,"XTick", [0])
set(gca,"YTick", [])
ylabel("amplitude")
xlabel("frequency")
%=======================================================
% Sample S(f) to portray Fourier series coefficients
subplot("position",[x_origin2 y_origin1 width height])
stem(X(1:128:end), Y(1:128:end), "-", "Color",[0 .4 .6]);
set(findobj("Type","line"),"Marker","none")
xlim(xlimits);
ylim([0 1.05]);
set(gca,"XTick", [0])
set(gca,"YTick", [])
ylabel("amplitude")
%xlabel("frequency")
box on
%=======================================================
% Sample the DTFT to portray a DFT
FFT_indices = [32:55]*128+1;
DFT_indices = [0:31 56:63]*128+1;
subplot("position",[x_origin2 y_origin2 width height])
stem(X(DFT_indices), Z(DFT_indices), "-", "Color",[0 .4 .6]);
hold on
stem(X(FFT_indices), Z(FFT_indices), "-", "Color","red");
set(findobj("Type","line"),"Marker","none")
xlim(xlimits);
ylim([0 1.05]);
set(gca,"XTick", [0])
set(gca,"YTick", [])
ylabel("amplitude")
xlabel("frequency")
box on
|
Pealdised
Lisa üherealine seletus sellest, mida fail esitab
A Fourier transform and 3 variations caused by periodic sampling (at interval T) and/or periodic summation (at interval P) of the underlying time-domain function.
Selles failis kujutatud üksused
kujutab
Teatud väärtus ilma Wikidata üksuseta
source of file inglise
original creation by uploader inglise
2. august 2014
media type inglise
image/gif
Faili ajalugu
Klõpsa kuupäeva ja kellaaega, et näha sel ajahetkel kasutusel olnud failiversiooni.
| Kuupäev/kellaaeg | Pisipilt | Mõõtmed | Kasutaja | Kommentaar | |
|---|---|---|---|---|---|
| viimane | 23. august 2019, kell 15:18 | 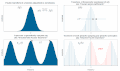 | 1128 × 672 (59 KB) | wikimediacommons>Bob K | re-color the portion of the DFT that is computed by the FFT |
Faili kasutus
Seda faili kasutab järgmine lehekülg:

