Mie hajumine

Mie hajumine on kui jätk Rayleigh' hajumisele, kus vastav teooria kehtib suurematele osakestele

Mie hajumine ehk Mie teooria on elektromagnetlainete hajumine kõige lihtsama kujuga isotroopsetelt osakestelt ehk sfääridelt, mille mõõtmed on vähemalt kümnendik nähtavast lainepikkusest. Teooria järgi peavad need osakesed paiknema homogeenses dielektrilises keskkonnas. Looduses esineb Mie hajumine osakestel, mille murdumisnäitaja on suurem kui üks. Kui muuta lainepikkust, muutub ka murdumisnäitaja.

Mie teooria on saanud nimetuse oma arendaja füüsik Gustav Mie (1867–1957) järgi. Kuigi oli ka teisi, kes varem samalaadseid probleeme lahendasid, nagu näiteks Taani füüsik Ludvig Lorenz, ei saanud nende artiklid nii palju tähelepanu kui Gustav Mie oma.

Kui osakesele langeva valguskiire lainepikkus on samas suurusjärgus osakese diameetriga, siis valgus interakteerub osakese ristlõikepindalaga, mis on suurem kui geomeetriline ristlõige osakesel. Geomeetrilise ristlõike all mõeldakse siin efektiivset piirkonda, kus toimub neeldumine või hajumine. Muutes mõjuva välja ristlõike suurust saame Mie teooria kaudu leida osakese geomeetrilise ristlõike $C_{scat}$. Sageli jagatakse see väärtus osakese ristlõikepindalaga, et väljendada hajumise efektiivsuse parameetrit $Q_{scat}$.

Sissejuhatus

Elektrilise dipooli järgu kasv osakese suuruse kasvades

Kuigi elektromagnetlainete hajumist sfäärilistelt osakestelt nimetatakse Mie teooriaks, polnud Gustav Mie esimene sellise probleemi püstitaja. Enne teda tegelesid sarnaste nähtustega teisedki teadlased, seetõttu on vanemates teadusallikates nimetatud neid lahendusi ka Lorenzi-Mie-Debye teooriaks ja Lorenzi-Mie teooriaks. Kaks nimetatud teooriat pole sisu poolest küll päris samad mis Mie teooria.

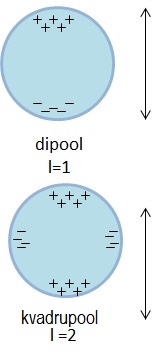
Kui sfäärilisele osakesele langeb elektromagnetlaine, siis iga elektron osakeses hakkab võnkuma selle elektromagnetlainega samas faasis. Võnkuvad elektronid kujutavad osakese sees elektrilist dipoolmomenti. Vastavalt elektromagnetismile kiirgab võnkuv elektron elektromagnetilist kiirgust samal sagedusel nagu võnkuv elektron. See kiirgus kajastabki hajuvat valgust. Teisalt, kui osakese mõõtmed on suuremad või samas suurusjärgus nähtava lainepikkusega, siis hakkavad elektronid eri osades erinevalt võnkuma. See omakorda põhjustab hajutatud valguse interferentsi, mis tekib eri osades olevatelt elektronidelt. Sellest sõltuvalt erineb hajutatud valguse amplituud ja nurkjaotus elektrilisest dipoolmomendist.Järelikult võib Mie teooriat kujutada kui teooriat, mis seletab, kuidas valgus hajub suurematelt osakestelt elektrilise dipoolmomendi, kvadrupoolmomendi või veel kõrgemat järku kiirgamisvõimaluste superpositsioonina. Selline lähenemisviis kehtib ka magnetväljade osakeste puhul.

Numbriline lahendamine

Enamik tänapäevastest lahendustest Mie teooria jaoks sarnanevad matemaatiliste seeriate lähendamisega Maxwelli võrranditele. Seeriate lahendamiseks kasutatakse mitmeid programmipakette, kus saab arvutada Mie teooria väärtusi (Fortran, Matlab, Mathematica,C). Peale valguse hajumise võimaldavad need programmipaketid arvutada matemaatilisete seeriate abil faasi hajumise funktsiooni, neeldumist, ekstinktsiooni, neeldumise efektiivsust ja muid sarnaseid parameetreid. Lisaks sfääriliste osakestele, saab sel viisil nende programmipakettidega leida eelnevaid parameetreid kontsentrilistele sfääridele, lõpmatu suurusega silindritele, sfäärilistele klastritele ja silindrilistele klastritele. On ka valemeid ellipsoidiliste osakeste parameetrite arvutamiseks. Veelgi üldisema kujuga osakeste puhul sobib arvutamiseks T-maatriks, kuid see meetod toetub Maxwelli võrrandite lähendamisele.

Maxwelli võrrandite kasutamine

Nii Rayleigh' hajumine kui ka Mie hajumine on elektromagnetlaine elastne hajumine osakestelt. Põhiline erinevus nende kahe vahel on see, et Rayleigh' hajumine toimub ainult valguskiire lainepikkusest palju väiksemate osakeste puhul. Seega võib Mie hajumist vaadelda kui selle probleemi lahenduse jätku. Rayleigh' teooria kehtib osakestele, mille mõõtmed on vahemikus

$a\ll \frac{\lambda }{2\pi n_m|m|}$

$|m|$ tähistab osakese absoluutset murdumisnäitajat ning $n_m$ keskkonna murdumisnäitajat. Reaalsete parameetritega peaks Rayleigh' hajumine töötama kulla osakeste puhul kuni osakesteni, mille mõõtmed on 40 nm. Osakese dimensioonitu karakteerse mõõtme parameeter avaldub raadiuse a ja sellele langeva lainepikkuse λ suhtes järgnevalt:

$x=\frac{2\pi n_m}{\lambda }$

$n_m$/λ on pealelangeva valguse dispersioon. Osake võib aga olla ka kompleksse murdumisnäitajaga, mispuhul see avaldub kui

$m=(n+ik)$

Kui valgusenergia läbib osakest, saab selle muutumiskiiruse kindlaks määrata, rakendades kompleksset Poyntingi vektori seadust. Selle seaduse kasutamisel saab leida hajumise ja ekstinktsiooni läbilõiked, mis avalduvad suhetena

$C_{ext}=\frac{W_{ext}}{I_{inc}}$

$C_{scat}=\frac{W_{scat}}{I_{inc}}$,

kus $I_{inc}$ tähistab intensiivsust alguspunktis. $W_{scat}$ ning $W_{ext}$ on vastavalt hajunud ja ekstinktsiooni energia, mille valemid on järgmised:

$W_{sca}=\frac{1}{2}Re\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{\pi }{\int }}(E_{sca}\times H_{sca}^{*})r^2\sin (\theta )d\theta d\varphi =\frac{1}{2}Re\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{\pi }{\int }}(E_{sca,\theta }\times H_{sca,\varphi }^{*}-E_{sca,\varphi }\times H_{sca,\theta }^{*})r^2\sin (\theta )d\theta d\varphi$

$W_{ext}=\frac{1}{2}Re\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{\pi }{\int }}(E_{inc}\times H_{sca}^{*})r^2\sin (\theta )d\theta d\varphi$

Neelatud energia on seotud hajunud ja ekstinktsiooni energiatega $W_{abs}=W_{ext}-W_{sca}$. Kasutades eelnevat nelja valemit üksteise suhtes, saab hajunud ja ekstinktsiooni läbilõike valemid:

$C_{sca}=\frac{2\pi }{k^2}\sum _{l=1}^{\mathrm{\infty }}(2l+1)(a_l|H_{l,m}{|}^2+b_l|F_{l,m}{|}^2)$

$C_{ext}=\frac{2\pi }{k^2}\sum _{l=1}^{\mathrm{\infty }}Re(2l+1)(a_l|H_{l,m}{|}^2+b_l|F_{l,m}{|}^2)$

Lihtsustuseks on kasutatud $k=\frac{2\pi n_m}{\lambda }$. Pöördenurga funktsioonide $F_{l,m}$ ja $H_{l,m}$ valemid on järgmised:

$F_{l,m}=\frac{2}{l}(l+1)\sum _{m=-l}^l\frac{(l-m)!}{(l+m)!}|{\rho }_{l,m}{|}^2$

$H_{l,m}=\frac{2}{l}(l+1)\sum _{m=-l}^l\frac{(l-m)!}{(l+m)!}|T_{l,m}{|}^2$

${\rho }_{l,m}=\frac{d{P}_{l,m}}{d\theta }$ ja $T_{l,m}=m\frac{P_{l,m}}{\sin (\theta )}$

$\theta$ kujutab valguse hajumisnurka ja $P_{l,m}$ on Legendre'i polünoom, mida kasutatakse rekursiivsetes funktsioonides.

Nurgast sõltuvaid Legendre'i polünoome saab arvutada järgmiste valemitega:

$P_{l+1}^m=\frac{1}{l-m+1}((2l+1)\cos (\theta )P_l^m-(l+m)P_{l-1}^m)$

$m\frac{P_{l,m}}{\sin (\theta )}=\frac{1}{2\cos (\theta )}(P_l^{m+1}+(l(l+1)-m(m-1))P_l^{m-1})$

$\frac{d{P}_{l,m}}{d\theta }=\frac{1}{2}(l-m+1(l+m)P_l^{m-1}+P_l^{m+1})$

Legendre'i polünoomide algsete väärtuste arvutamiseks saab kasutada valemeid

$P_l^m(x)=(-1{)}^m(1-x^2{)}^{m/2}\frac{d^m}{d{x}^m}(P_l(x))$

$P_l(x)=\frac{1}{2^{l}l!}\frac{d^l}{d{x}^l}[(x^2-1{)}^l],$

kus tasalainete korral peab arvestama ainult esimest järku $(m=1)$. Seejärel taanduvad hajunud ja ekstinktsiooni läbilõike valemid kujule:

$C_{sca}=\frac{2\pi }{k^2}\sum _{l=1}^{\mathrm{\infty }}(2l+1)(|a_{l,m}{|}^2+|b_{l,m}{|}^2)$

$C_{ext}=\frac{2\pi }{k^2}\sum _{l=1}^{\mathrm{\infty }}Re(2l+1)(|a_{l,m}{|}^2+|b_{l,m}{|}^2)$

Tuleb rõhutada, et lühiajaliste lainete puhul, mille ergastamise langemisnurk on tasapinna suhtes suurem kui null, lisandub veel nurga parameetreid, mis muudab valemi pikemaks. Mie koefitsiendid $a$ ja $b,$ mis põhjustavad hajunud välja laienemist, saab leida ääretingimustest, mis rahuldaksid Maxwelli võrrandeid. Lahendades need ära, võib jõuda tulemusele:

$a_n=\frac{\psi {\text{'}}_n(mx)\psi (x)-m{\psi }_n(mx)\psi {\text{'}}_n(x)}{m\psi {\text{'}}_n(mx)\xi (x)-m{\psi }_n(mx){\xi }^{\prime }(x)}$

$b_n=\frac{m\psi {\text{'}}_n(mx)\psi (x)-{\psi }_n(mx)\psi {\text{'}}_n(x)}{m\psi {\text{'}}_n(mx)\xi (x)-{\psi }_n(mx){\xi }^{\prime }(x)}$

$\psi (z{)}_l=\sqrt{\pi \frac{z}{2}}J(z{)}_{l+0.5}$ ja $\xi (z{)}_l=\sqrt{\pi \frac{z}{2}}(J(z{)}_{l+0.5}+iN(z{)}_{l+0.5})$ on Riccati-Besseli võrrandid ning ${\psi }^{\prime }(z)$ ja ${\xi }^{\prime }(z)$ on nende esimest järku tuletised. $J$ on vastavalt esimest järku sfääriline Besseli funktsioon ning $N$ on teist järku sfääriline Besseli võrrand. Kui keskkond ise on kompleksse murdumisnäitajaga, tuleb võrrandeid modifitseerida.

Mie hajumine looduses

Just tänu Mie hajumisele näeme pilvi sellisena, nagu need pildil on

Mie hajumine ei ole tugevalt valguse lainepikkusest sõltuv ja just seetõttu võib näha näiteks rünkpilvi valgetena ning udu valkjashallina. Pilvede aluspind on aga valguse neeldumise tõttu tumedam. Teiseks sõltub valguse hajumine lumel temperatuurist, seega on sulamispiirist madalamal temperatuuril pilved ja udu valgemad. Hajumine ise jaotatakse elastseks ja mitteelastseks. Rayleigh ja Mie hajumine on elastsed, sest osakeste põrgete tulemusel jääb laine kuju samasuguseks. Vastasel juhul võiks Rayleigh' hajumist mõista kui õhus olevatelt osakestelt saadavat soojuskiirgust ja Mie hajumist kui pilvedelt ja udult saadavat soojuskiirgust.

Rakendused

Mie hajumine on oluline metroloogilises optikas, kus nähtava valguslaine ja osakeste vahelised suhted on karakteersed väärtused probleemidele, mis sõltuvad keskkonna hägususest ja valguse hajumisest pilvedelt. Samuti aitab Mie teooria mõista tavapäraste ainete (nt piim, kude ja udu) välimust.

Osakeste omaduste uurimiseks

Pildil on modelleeritud raadiusega 220 nm kullast nanosfäär, mis paikneb vees. Antud parameetritega on leitud Mie hajumise spekter. Tulemusena on spektris näha kolm dipooli järku

Mie teooria valemite abil püütakse iseloomustada osakesi vastavalt nende hajumisele. Metalliliste osakeste puhul proovitakse üles leida vastavalt osakese suurusest sõltuv lokaliseeritud plasmonresonants. Kui osake on piisavalt väike, siis tekib Rayleigh' hajumisteooria järgi spektris ainult üks resonants. Suurendades raadiust, suureneb võimalike resonantsolukordade arv vastavalt sellele, kui mitu elektrilise dipooli järku leidub.

Tööstuses

Viimastel aastatel on proovitud rakendada hajumise valemeid ning uurida, kuidas tõsta päikesepaneelide efektiivsust. Üks võimalus selleks on lisada kullast nanoosakesi ja vastavalt nende suurustele tuleb mängu Mie või Rayleigh' hajumine.

Meditsiinis

Mie teooriat on samuti kasutatud valguse hajumise määramiseks, et leida, kas tegemist on terve või vähktõbise rakuga.

Metamaterjalid

Mie teooria alusel on valmistatud dielektrilisi metamaterjale. Metamaterjal on materjal, mida looduses ei leidu ja millel võib olla negatiivne magnetiline läbitavus. Need metamaterjalid koosnevad kolmemõõtmelistest komposiitidest, kas metallist või mittemetallist. Komposiidid on perioodiliselt või juhuslikult kokku pakitud madala magnetilise läbitavusega maatriksiks. Sellises skeemis on negatiivsed olemuslikud parameetrid loodud nii, et need tekiks Mie resonantsolukordade ümbruses.Efektiivne magnetiline läbitavus tekib selliste olukordade ümbruses, kus esineb Mie elektrilise dipooli hajumise koefitsient. Efektiivne dielektriline läbitavus aga tekib selliste olukordade ümbruses, kus esineb Mie magnetilise dipooli hajumise koefitsient.

Kontsentratsiooni ja osakeste suuruse määramiseks

Iga metallist nanoosakese puhul tekib plasmonresonants erineval lainepikkusel. Osakese diameetri suurendamisel toimub aga punanihe ehk resonantsi tipu nihkumine paremale. Samal ajal tekivad erinevad dipoolid. Kui on veel teada hajunud valguse intensiivsus, siis saab kasutada Beeri-Lamberti seadust, et määrata uuritavate osakeste kontsentratsiooni.

Vaata ka

• Hajumine
• Rayleigh' hajumine

Välislingid

• Mieplot – arvutiprogramm, millega saab leida hajumist sfääris Mie & Deye seeriate alusel
• MieCalc – vabalt seadistatav programm valguse hajumise arvutusteks
• Kollektsioon valguse hajumise koodidest