Sirge: erinevus redaktsioonide vahel
imported>InternetArchiveBot Lisatud 1 allikale arhiivilink ja märgitud 0 mittetöötavaks.) #IABot (v2.0.8.8 |
(Erinevus puudub)
|
Viimane redaktsioon: 30. juuni 2022, kell 06:21
Mall:ToimetaAeg Mall:KeeletoimetaMall:TOCright Sirge ehk sirgjoon on ilma läbimõõduta, mõlemas suunas lõpmata pikk, kõverusteta joon ehk ühemõõtmeline ruum, mis võib sisalduda mitmemõõtmelises ruumis[1].
Sirge tasandil
Üldvõrrand
Sirge üldvõrrand tasandil on (Descartesi koordinaadistikus) ristkoordinaadistikus lineaarvõrrand , kus , ja on konstandid, kusjuures ja ei võrdu samaaegselt nulliga.
Näide
Sirge võrrand tasandil:
Parameetriline kuju
Kasutatakse üldvõrrandi parameetrilist kuju [2][3]
Näide
, kus sirge on määratud 2 vektori kaudu :
või
Lisaks eelnimetatule on võimalik parameetrilist kuju tähistada, kui parameetrilisi võrrandeid
ja (Descartesi kujul) ehk kanoonilisel kujul
Joonised
-
Võrrandiga määratud sirge.
-
Parameetrilise võrranditega , määratud sirge.
-
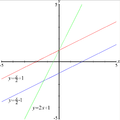
Sirged tasandil.
Omadused
Olgu antud sirged ja , ning nendele vastavad sihivektorid ja .
Ristuvad sirged
Sirged on risti parajasti siis, kui nende sihivektorite tadamskalaarkorrutis on :
Paralleelsed sirged
Sirged on paralleelsed parajasti siis, kui nende sihivektorite skalaarkorrutise moodul on :
Kahte punkti saab läbida vaid üks sirge
Eukleidese geomeetrias läbib kahte eri punkti parajasti üks sirge.
Määratud
tõusu ja algordinaadiga
Tõusu (k) ja algordinaadiga (a) määratud sirge võrrand tasandil:
- .
kahe punktiga
Kahe punktiga määratud sirge võrrand tasandil:
- .
punkti ja sihivektoriga
Punkti ja sihivektoriga määratud sirge võrrand tasandil:
- .
punkti ja tõusuga
Punkti ja tõusuga määratud sirge võrrand tasandil:
- .
kahe tasandi lõikena
Kahe tasandi ja lõike sirge, kus on normaal vektor, on antud
kus
Rakendatavad funktsioonid
Sirge kaugus punktist ℝ3 ruumis
Olgu antud sirge ja punkt . Olgu sirge sihivektoriks , siis leiame punkti sirgel, mis asub sirgel ja mille kaugus on vähim punkti . Selleks lahendame võrrandid :
Siis leiame vektori ja selle pikkuse , mis on punkti kaugus sirgest:
Sirgete kaugus ruumis
Olgu antud sirged ja . Sellest leiame vastavad sihivektorid ning ja suvalised punktid mõlemal sirgel vastavalt ja .